Oct-Nov-21-p2-CIE-4037-22 : Solution
2021 (Oct-Nov) CIE (4037-Additional Mathematics), Paper 2/22 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို Download ယူနိုင်ပါသည်။
(a) On the axes, draw the graphs of $y=5+|3 x-2|$ and $y=11-x$.
[4]
(b) Using the graphs, or otherwise, solve the inequality $11-x < 5+|3 x-2|$.
[2]
(a) Expand $(2-3x)^4$, evaluating all of the coefficients.
[4]
(b) The sum of the first three terms in ascending powers of $x$ in the
expansion of $(2-3 x)^{4}\left(1+\dfrac{a}{x}\right)$ is $\dfrac{32}{x}+b+c x$,
where $a, b$ and $c$ are integers. Find the values of each of $a, b$ and $c .$
[4]
(a) Show that $\dfrac{1}{\sec x-1}+\dfrac{1}{\sec x+1}=2 \cot x \operatorname{cosec} x$.
[4]
(b) Hence solve the equation $\dfrac{1}{\sec x-1}+\dfrac{1}{\sec x+1}=3 \sec x$
for $0^{\circ} < x < 360^{\circ}$.
[4]
SOLUTION
(a) Find the $x$-coordinates of the stationary points on the curve
$y=3 \ln x+x^{2}-7 x$, where $x>0$.
[5]
(b) Determine the nature of each of these stationary points.
[3]
(a) Solve the following simultaneous equations.
$\begin{aligned}
&\\
\qquad e^{x}+e^{y}&=5 \\\\
\qquad 2 e^{x}-3 e^{y}&=8
\end{aligned}$
[5]
(b) Solve the equation $e^{(2 t-1)}=5 e^{(5 t-3)}.$
[4]
DO NOT USE A CALCULATOR IN THIS QUESTION.
All lengths in this question are in centimetres.
You may use the following trigonometrical ratios.
$\begin{aligned}
&\\
\qquad &\sin 60^{\circ}=\dfrac{\sqrt{3}}{2} \\\\
\qquad &\cos 60^{\circ}=\dfrac{1}{2} \\\\
\qquad &\tan 60^{\circ}=\sqrt{3}\\\\
\end{aligned}$
The diagram shows triangle $A B C$ with $A C=\sqrt{6}-\sqrt{2},
A B=\sqrt{6}+\sqrt{2}$ and angle $C A B=60^{\circ}$.
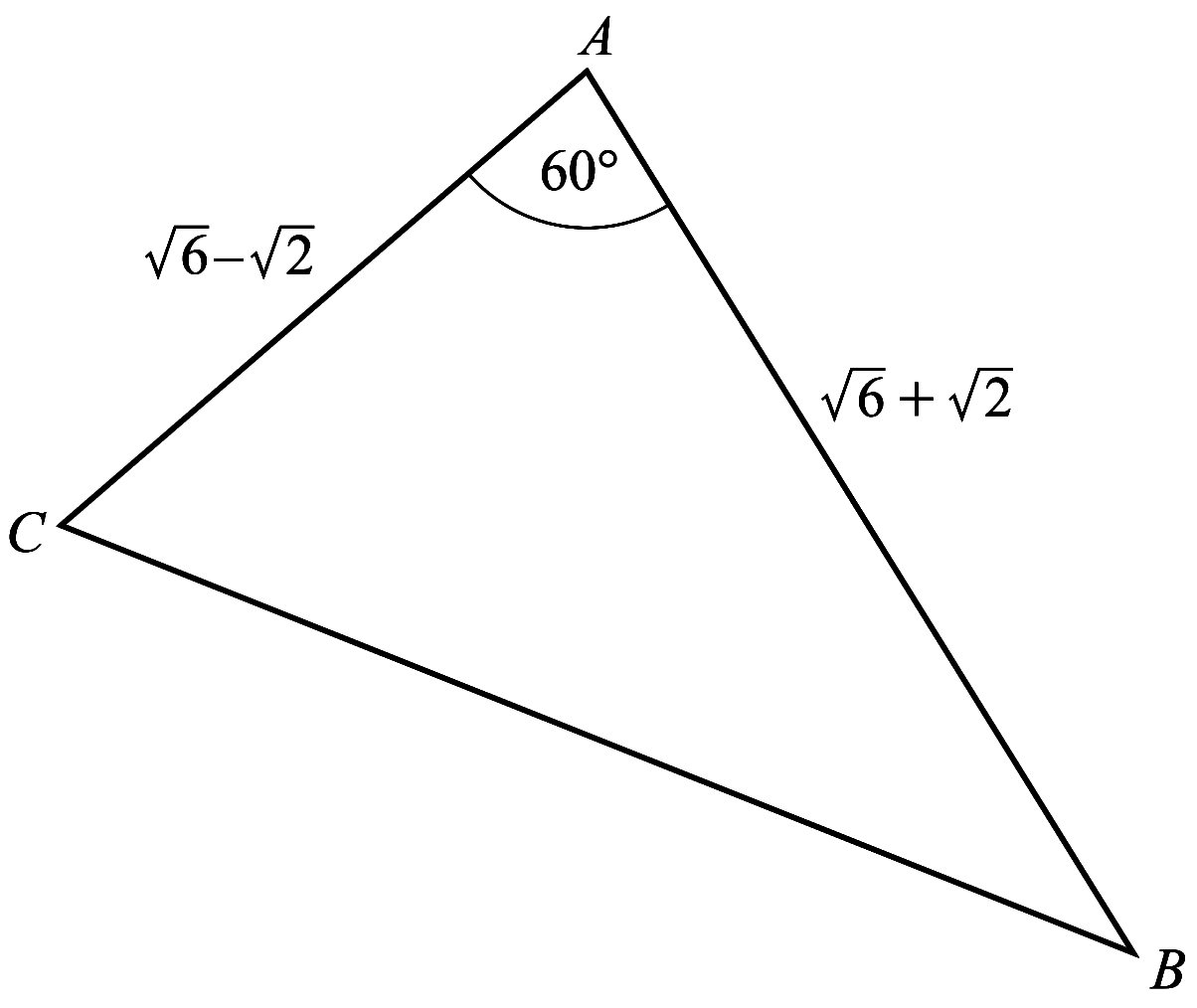
(a) Find the exact length of $B C$.
[3]
(b) Show that $\sin A C B=\dfrac{\sqrt{6}+\sqrt{2}}{4}$.
[2]
(c) Show that the perpendicular distance from $A$ to the line $B C$ is $1$.
[2]
It is given that $\dfrac{d^{2} y}{dx^{2}}=e^{2 x}+\dfrac{1}{(x+1)^{2}}$ for $x>-1$.
(a) Find an expression for $\dfrac{dy}{dx}$ given that $\dfrac{d y}{dx}=2$ when $x=0$.
[3]
(b) Find an expression for $y$ given that $y=4$ when $x=0$.
[3]
SOLUTION
Variables $x$ and $y$ are such that when $\sqrt{y}$ is plotted against
$\log _{2}(x+1)$, where $x>-1$, a straight line is obtained which passes
through $(2,10.4)$ and $(4,15.4)$.
(a) Find $\sqrt{y}$ in terms of $\log _{2}(x+1)$.
[4]
(b) Find the value of $y$ when $x=15$.
[1]
(c) Find the value of $x$ when $y = 25$.
[3]
(a) Find the equation of the normal to the curve $y=x^{3}+x^{2}-4 x+6$ at
the point $(1,4)$.
[5]
(b) DO NOT USE A CALCULATOR IN THIS QUESTION.
Find the exact $x$-coordinate of each of the two points where
the normal cuts the curve again.
[5]
(a) The first three terms of an arithmetic progression are $x, 5x-4$ and
$8x+2$. Find $x$ and the common difference.
[4]
(b) The first three terms of a geometric progression are $y, 5y-4$ and $8y+2$.
(i)) Find the two possible values of $y$.
[4]
(ii)) For each of these values of $y$, find the corresponding value of the common ratio.
[2]
SOLUTION
SOLUTION
$\begin{aligned}
&y=5+|3 x-2| \\\\
&y=3\left|x-\frac{2}{3}\right|+5 \\\\
\therefore\ & \text { vertex }=\left(\frac{2}{3}, 5\right) \\\\
&\text { When } x=0, y=7 \\\\
\therefore\ & y \text {-intercept }=(0,7)\\\\
&y=11-x\\\\
&\text { When } x=0, y=11 \\\\
\therefore\ & y-\text {-intercept } =(0,11)\\\\
&\text { When } y=0, x=11 \\\\
\therefore\ & x-\text {-intercept } =(11,0)\\\\
\end{aligned}$
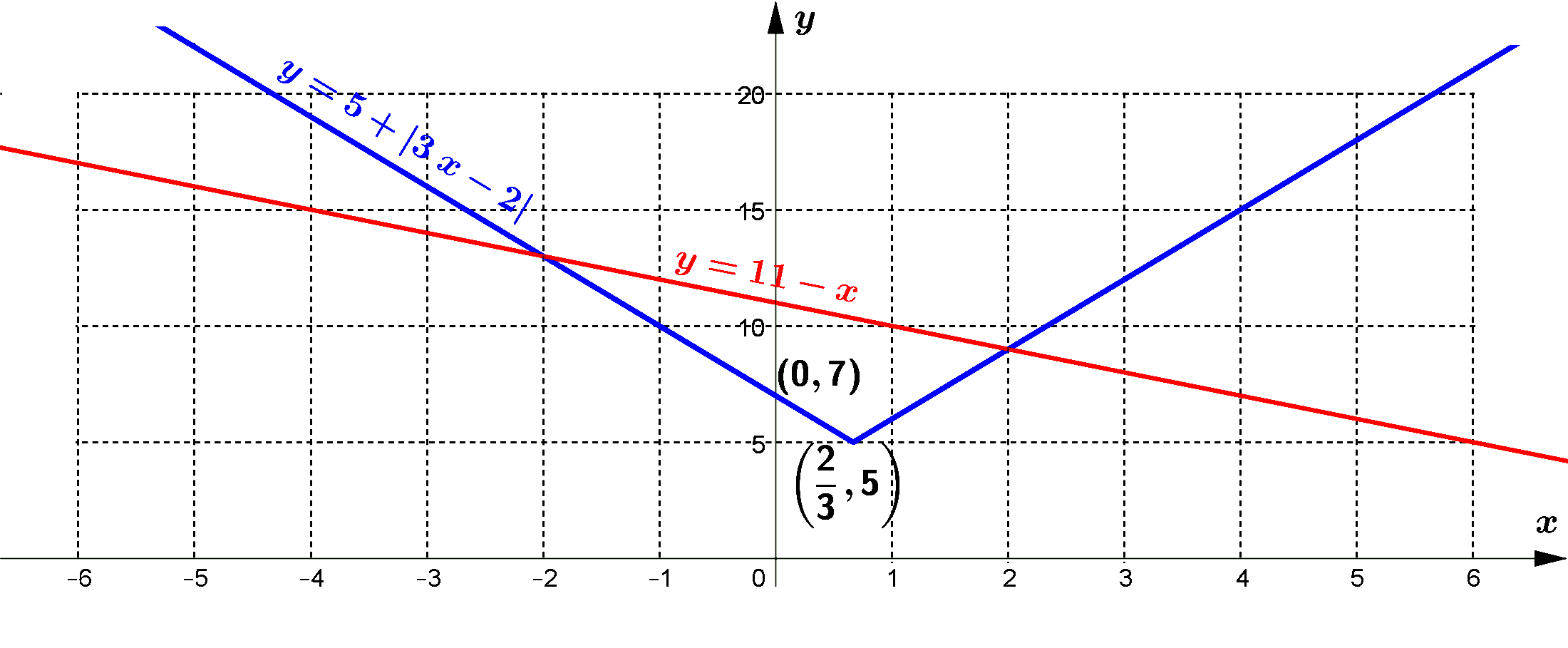
According to the graph, the solution set to satisfy the inequality $1-x < 5+| 3 x-2|$ is $\{x \mid x <-2 \text { or } x>2\}$.
SOLUTION
$\begin{aligned}
(2-3 x)^{4} &=2^{4}+4\left(2^{3}\right)(-3 x)+6\left(2^{2}\right)(-3 x)^{2}+4(2)(-3 x)^{3}+(-3 x)^{4} \\\\
&=16-96 x+216 x^{2}-24 x^{3}+81 x^{4} \\\\
\end{aligned}$
$\begin{aligned}
(2-3 x)\left(1+\frac{a}{x}\right) &=\frac{32}{x}+b+c x+\cdots \\\\
\left(16-96 x+216 x^{2}-24 x+81 x^{4}\right)\left(1+\frac{a}{x}\right) &=\frac{32}{x}+b+c x+\cdots \\\\
16+\frac{16 a}{x}-96 x-96 a+216 a x+\cdots &=\frac{32}{x}+b+c x+\cdots \\\\
\frac{16 a}{x}+(16-96 a)+(216 a-96) x+\cdots &=\frac{32}{x}+b+c x+\cdots \\\\
\end{aligned}$
$\begin{aligned}
\therefore\ & 16 a =32, a=2 \\\\
& b =16-96 a=-176 \\\\
& c =216 a-96=336
\end{aligned}$
$\begin{aligned}
& \frac{1}{\sec x-1}+\frac{1}{\sec x+1} \\\\
=&\ \frac{\sec x+1+\sec x-1}{(\sec x-1)(\sec x+1)} \\\\
=&\ \frac{2 \sec x}{\sec ^{2} x-1} \\\\
=&\ \frac{2 \sec x}{\tan ^{2} x} \\\\
=&\ 2 \cdot \frac{1}{\cos x} \frac{1}{\tan x} \frac{1}{\tan x}\\\\
=&\ \cdot \frac{1}{\cos x} \cdot \frac{\cos x}{\sin x} \cdot \cot x \\\\
=&\ \frac{2}{\sin x} \cdot \cot x \\\\
=&\ 2\cot x \operatorname{cosec} x\\\\
\end{aligned}$
$\begin{aligned}
\frac{1}{\sec x-1}+\frac{1}{\sec x+1} &=3 \sec x, 0^{\circ}<x<360^{\circ} \\\\
2 \cot x \operatorname{cosec} x &=3 \sec x \\\\
2 \frac{\cos x}{\sin x} \frac{1}{\sin x} &=\frac{3}{\cos x} \\\\
2 \cos ^{2} x &=3 \sin ^{2} x \\\\
\tan ^{2} x &=\frac{2}{3} \\\\
\tan x &=\pm \frac{2}{3} \\\\
x &=39.2^{\circ} \text { or } \\\\
x &=140.8^{\circ} \text { or } \\\\
x &=219.2^{\circ} \text { or } \\\\
x &=320.8^{\circ}
\end{aligned}$
SOLUTION
$\begin{aligned}
\text{(a) }\quad &y=3 \ln x+x^{2}-7 x \\\\
&\frac{d y}{d x}=\frac{3}{x}+2 x-7 \\\\
&\frac{d y}{d x}=0 \text { when, } \\\\
&\frac{3}{x}+2 x-7=0 \\\\
&2 x^{2}-7 x+3=0 \\\\
&(2 x-1)(x-3)=0 \\\\
&x=\frac{1}{2} \text { or } x=3\\\\
\end{aligned}$
$\qquad$ Hence, the curve has stationary points where $x=\dfrac{1}{2}$ or $x=3$.
$\begin{aligned}
&\\
\text{(b) }\quad &\frac{d^{2} y}{d x^{2}}=-\frac{3}{x^{2}}+2\\\\
&\text { When } x=\frac{1}{2}, \frac{d^{2} y}{d x^{2}}=-\frac{3}{\frac{1}{4}}+2=-10<0 \\\\
&\text { When } x=3, \frac{d^{2} y}{d x^{2}}=-\frac{3}{9}+2=\frac{5}{3}>0\\\\
\end{aligned}$
$\therefore\quad$ The curve is maximum where $x=\dfrac{1}{2}$ and is minimum where $x=3.$
SOLUTION
$\begin{aligned}
\text{ (a) }\hspace{1.5cm} e^{x}+e^{y}&=5 \\\\
e^{y} &=5-e^{x} \\\\
2 e^{x}-3 e^{y}&=8 \\\\
\therefore\ 2 e^{x}-3\left(5-e^{x}\right) &=8 \\\\
2 e^{x}-15+3 e^{x} &=8 \\\\
5 e^{x} &=23 \\\\
e^{x} &=\frac{23}{5} \\\\
x &=\ln \left(\frac{23}{5}\right) \\\\
&=1.53\\\\
e^{y} &=5-\frac{23}{5} \\\\
&=\frac{2}{5} \\\\
y &=\ln \left(\frac{2}{5}\right) \\\\
&=-0.916\\\\
\text{ (b) }\hspace{1.5cm}\frac{e^{(2 t-1)}}{e^{2 t-1}} &=5 e^{(5 t-3)} \\\\
e^{5 t-3} &=5 \\\\
\frac{1}{e^{3 t}-2} &=5 \\\\
e^{3 t-2} &=\frac{1}{5} \\\\
3 t-2 &=\ln \frac{1}{5} \\\\
t &=\frac{1}{3}\left(2+\ln \frac{1}{5}\right) \\\\
&=0.13
\end{aligned}$
SOLUTION
$\text { (a) }$ By cosine Rule,
$\begin{aligned}
&\\
\qquad BC^{2} &=A B^{2}+A C^{2}-2(A B)(A C) \cos A \\\\
&=(\sqrt{6}+\sqrt{2})^{2}+(\sqrt{6}-\sqrt{2})^{2}-2(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2}) \cos 60^{\circ} \\\\
&=6+2 \sqrt{12}+2+6-2 \sqrt{12}+2-2(6-2) \frac{1}{2} \\\\
&=12 \\\\
B C &=\sqrt{12} \\\\
B C &=2 \sqrt{3}\\\\
\end{aligned}$
$\text { (b) }$ By Sine Rule,
$\begin{aligned}
&\\
\qquad \frac{\sin (\angle A C B)}{A B} &=\frac{\sin (\angle B A C)}{B C} \\\\
\sin (\angle A C B) &=\frac{A B}{B C} \sin (\angle B A C) \\\\
&=\frac{\sqrt{6}+\sqrt{2}}{2 \sqrt{3}} \times \sin 60^{\circ} \\\\
&=\frac{\sqrt{6}+\sqrt{2}}{2 \sqrt{3}} \times \frac{\sqrt{3}}{2} \\\\
&=\frac{\sqrt{6}+\sqrt{2}}{4}\\\\
\end{aligned}$
$\text { (c) }$ Let $h$ be the perpendicular distance from $A$ to $B C$.
$\begin{aligned}
&\\
\qquad \therefore\ h &=A C \sin (\angle A C B) \\\\
&=(\sqrt{6}-\sqrt{2}) \frac{\sqrt{6}+\sqrt{2}}{4} \\\\
&=\frac{6-2}{4} \\\\
&=1
\end{aligned}$
$\begin{aligned}
\frac{d^{2} y}{d x^{2}}=e^{2 x} &+\frac{1}{(x+1)^{2}}, x>-1 . \\\\
\therefore \frac{d y}{d x} &=\displaystyle\int\left(e^{2 x}+\frac{1}{(x+1)^{2}}\right) d x \\\\
&=\frac{1}{2} \displaystyle\int e^{2 x} d(2 x)+\displaystyle\int(x+1)^{-2} d x \\\\
&=\frac{1}{2} e^{2 x}-\frac{1}{x+1}+c_{1} \\\\
\frac{d y}{d x} &=2 \text{ when }x=0\\\\
\frac{1}{2}-1+e_{1} &=2 \\\\
c_{1} &=\frac{5}{2} \\\\
\therefore\ \frac{d y}{d x} &=\frac{1}{2} e^{2 x}-\frac{1}{x+1}+\frac{5}{2}\\\\
y &=\displaystyle\int\left[\frac{1}{2} e^{2 x}-\frac{1}{x+1}+\frac{5}{2}\right] d x \\\\
&=\displaystyle\int \frac{1}{2} e^{2 x} d x-\displaystyle\int \frac{1}{x+1} d x+\frac{5}{2} \displaystyle\int d x \\\\
&=\frac{1}{4} e^{2 x}-\ln (x+1)+\frac{5 x}{2}+c_{2} \\\\
y &=4 \text { when } x=0 \\\\
\therefore\ \frac{1}{4}+c_{2} &=4 \\\\
\therefore\ c_{2} &=\frac{15}{4}\\\\
\therefore\ y&=\frac{1}{4} e^{2 x}-\ln (x+1)+\frac{5 x}{2}+\frac{15}{4}
\end{aligned}$
SOLUTION
$ \text{ (a) }\quad$ The straight line passes through the points $(2,10.4)$ and $(4,15.4)$.
$\begin{aligned}
&\\
\qquad\therefore \text{ gradient } &=\frac{15 \cdot 4-10 \cdot 4}{4-2}\\\\
&=\frac{5}{2}\\\\
\end{aligned}$
$\quad \therefore\ $ Equation of straight line is
$\begin{aligned}
&\\
\quad \sqrt{y}-10.4 &=\frac{5}{2}\left(\log _{2}(x+1)-2\right) \\\\
\sqrt{y} &=\frac{5}{2} \log _{2}(x+1)+5-4\\\\
\text{ (b) }\quad \text{ When } x&=15,\\\\
\sqrt{y} &=\frac{5}{2} \log _{2}(16)+5.4 \\\\
&=\frac{5}{2}(4)+5.4 \\\\
&=15.4 \\\\
y &=237.16\\\\
\text{ (c) }\quad \text{ When } y&=25,\\\\
\sqrt{25} &=\frac{5}{2} \log _{2}(x+1)+5.4 \\\\
\log (x+1) &=-0.16 \\\\
x+1 &=2^{-0.16} \\\\
x &=2^{-0.16}-1 \\\\
&=-0.105
\end{aligned}$
SOLUTION
$\begin{aligned}
\text{ (a) } \hspace{1.5cm}\text{ Curve } : y&=x^{3}+x^{2}-4 x+6\\\\
\frac{d y}{d x} &=3 x^{2}+2 x-4 \\\\
\left.\frac{d y}{d x}\right|_{(1,4)} &=3+2-4 \\\\
&=1\\\\
\therefore\ \text{ gradient of normal } &=-1\\\\
\end{aligned}$
$\qquad$ The equation of normal line at $(1,4)$ is
$\begin{aligned}
&\\
\quad y-4 &=-1(x-1) \\\\
y &=5-x\\\\
\end{aligned}$
$\text{ (b) } \quad$ At the point of intersection of normal and curve,
$\begin{aligned}
&\\
\qquad x^{3}+x^{2}-4 x+6&=5-x \\\\
x^{3}+x^{2}-3 x+1&=0\\\\
\end{aligned}$
$\begin{aligned}
\qquad \text{ Let } f(x)&=x^{3}+x^{2}-3 x+1\\\\
f(1) &=1+1-3+1 \\\\
&=0\\\\
\end{aligned}$
$\therefore(x-1)$ is a factor of $f(x)$.
$\begin{aligned}
&\\
\qquad &\text{ Let } f(x)=(x-1)\left(x^{2}+k x-1\right)\\\\
&\therefore\ x^{3}+x^{2}-3 x+1=(x-1)\left(x^{2}+k x-1\right)\\\\
\end{aligned}$
$\begin{aligned}
\qquad \text{ When } x =2,\quad &\\\\
8+4-6+1 &=(2-1)(4+2 k-1)\\\\
7&=3+2 k \\\\
k&=2\\\\
\end{aligned}$
$\begin{aligned}
\qquad \therefore\ (x-1)\left(x^{2}+2 x-1\right)&=0 \\\\
(x-1)\left(x^{2}+2 x+1-2\right)&=0 \\\\
(x-1)\left((x+1)^{2}-2\right)&=0 \\\\
\therefore x-1=0 \text { or }(x+1)^{2}-2&=0 \\\\
\therefore x=1 \text { or } x=-1 \pm &\sqrt{2}\\\\
\end{aligned}$
$\quad$ The normal cuts the curve again where
$x=-1-\sqrt{2}$ and $x=-1+\sqrt{2}$
$\text{ (a) }\quad x, 5 x-4$ and $8 x+2$ ane in an A.P.
$\begin{aligned}
&\\
\quad\therefore \quad 5 x-4-x &=8 x+2-5 x+4 \\\\
4 x-4 &=3 x+6 \\\\
\therefore \quad x &=10\\\\
\end{aligned}$
$\qquad$Let the common difference be $d$.
$\begin{aligned}
&\\
\quad\therefore\quad d &=5 x-4-x \\\\
&=4 x-4 \\\\
&=4(x-1) \\\\
&=4(10-1) \\\\
&=36\\\\
\end{aligned}$
$\text{ (b) }\quad y, 5 y-4$ and $8 y+2$ are in G.P.
$\begin{aligned}
&\\
\text{ (i) }\hspace{1.5cm} \therefore \frac{5 y-4}{y} &=\frac{8 y+2}{5 y-4} \\\\
\quad 25 y^{2}-40 y+16 &=8 y^{2}+2 y \\\\
17 y^{2}-42 y+16 &=0 \\\\
(17 y-8)(y-2) &=0 \\\\
\therefore y=\frac{8}{17} \text { or } y &=2\\\\
\end{aligned}$
$\text{ (ii) }\quad$ Let the common ratio be $r$,
$\begin{aligned}
&\\
\qquad\text{ When } y&=\frac{8}{17},\\\\
r &=\frac{5 y-4}{y} \\\\
&=\frac{5\left(\frac{8}{17}\right)-4}{\frac{8}{17}} \\\\
&=-\frac{7}{2}\\\\
\text{ When } y&=2,\\\\
r &=\frac{5 y-4}{y} \\\\
&=\frac{10-4}{2} \\\\
&=3
\end{aligned}$

Post a Comment for "Oct-Nov-21-p2-CIE-4037-22 : Solution"