Oct-Nov-21-p1-CIE-4037-12 : Solution
2021 (Oct-Nov) CIE (4037-Additional Mathematics), Paper 1/12 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။
The diagram shows the graph of the cubic function $y = f( x )$. The intercepts of the curve with the axes
are all integers.
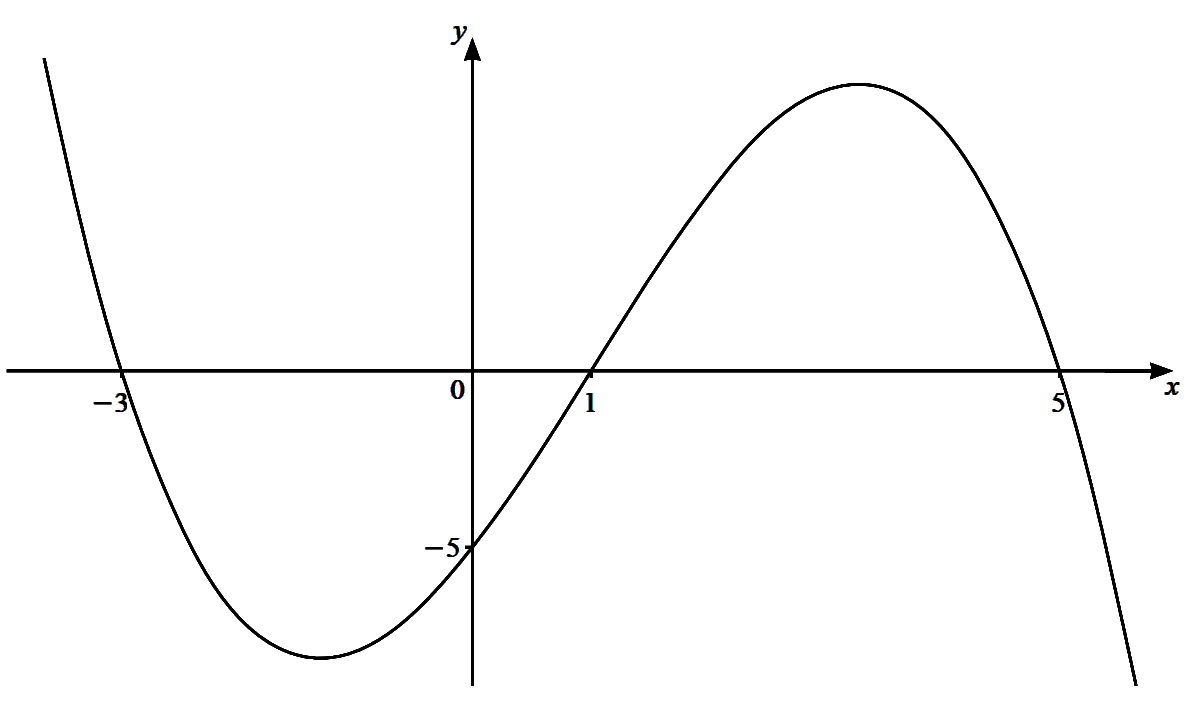
(a) Find the set of values of $x$ for which $f(x) < 0$.
[1]
(b) Find an expression for f(x).
[3]
SOLUTION
(a) Given that $\dfrac{\sqrt[3]{x y}(z y)^{2}}{(x z)^{-3} \sqrt{z}}=x^{a} y^{b} z^{c}$,
find the exact values of the constants $a, b$ and $c$.
[3]
(b) Solve the equation $5\left(2^{2 p+1}\right)-17\left(2^{p}\right)+3=0$.
[4]
SOLUTION
(a) Write $3+2 \lg a-4 \lg b$ as a single logarithm to base $10$ .
[4]
(b) Solve the equation $3 \log _{a} 4+2 \log _{4} a=7$.
[5]
Solve the equation $\cot \left(2 x+\dfrac{\pi}{3}\right)-\sqrt{3}=0$, where $-\pi<x<\pi$ radians.
Give your answers in terms of $\pi$.
[4]
Find the possible values of the constant $c$ for which the line $y=c$ is a tangent to the
curve $y=5 \sin \dfrac{x}{3}+4$.
[3]
DO NOT USE A CALCULATOR IN THIS QUESTION.
The polynomial $\mathrm{p}(x)=10 x^{3}+a x^{2}-10 x+b$, where $a$ and $b$ are integers, is divisible by $2 x+1$.
When $\mathrm{p}(x)$ is divided by $x+1$, the remainder is $-24$.
(a) Find the value of $a$ and of $b$.
[4]
(b) Find an expression for $p(x)$ as the product of three linear factors.
[4]
(c) Write down the remainder when $p(x)$ is divided by $x$.
[1]
(a)The diagram shows triangle $O A C$, where $\overrightarrow{O A}=\mathbf{a},
\overrightarrow{O B}=\mathbf{b}$ and $\overrightarrow{O C}=\mathbf{c}$.
The point $B$ lies on the line $A C$ such that $A B: B C=m: n$, where $m$ and $n$
are constants.
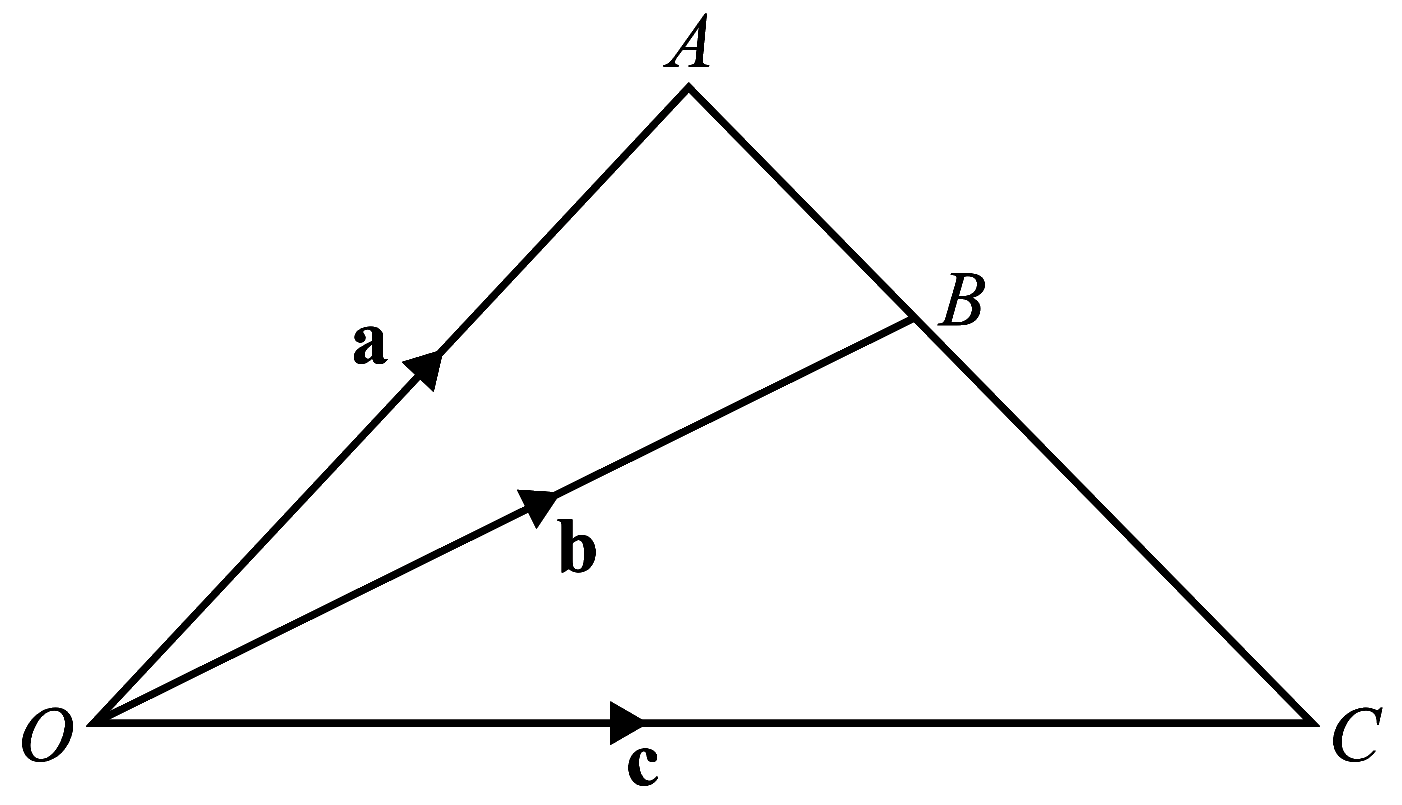
(i) Write down $\overrightarrow{A B}$ in terms of $\mathbf{a}$ and $\mathbf{b}$.
[1]
(ii) Write down $\overrightarrow{B C}$ in terms of $\mathbf{b}$ and $\mathbf{c}$.
[1]
(iii) Hence show that $n \mathbf{a}+m \mathbf{c}=(m+n) \mathbf{b}$.
[2]
(b) Given that $\lambda\left(\begin{array}{l}2 \\ 1\end{array}\right)+(\mu-1)\left(\begin{array}{r}-4 \\ 7\end{array}\right)=(\lambda+1)\left(\begin{array}{r}4 \\ -2\end{array}\right)$,
find the value of each of the constants $\lambda$ and $\mu$.
[4]
(a) A $5$-digit number is made using the digits $0, 1, 4, 5, 6, 7$ and $9$. No digit may be used more
than once in any $5$-digit number. Find how many such $5$-digit numbers are even and greater than
$50, 000$.
[3]
(b) The number of combinations of n objects taken $4$ at a time is equal to $6$ times the number of
combinations of $n$ objects taken $2$ at a time. Calculate the value of $n$.
[5]
The diagram shows a circle, centre $O$, radius $12 \mathrm{~cm}$, and a rectangle $A B C D$.
The diagonals $A C$ and $B D$ intersect at $O$. The sides $A B$ and $A D$ of the rectangle
have lengths $6 \mathrm{~cm}$ and $4 \mathrm{~cm}$ respectively. The points $M$ and $N$ lie
on the circumference of the circle such that $M A C$ and $N D B$ are straight lines.
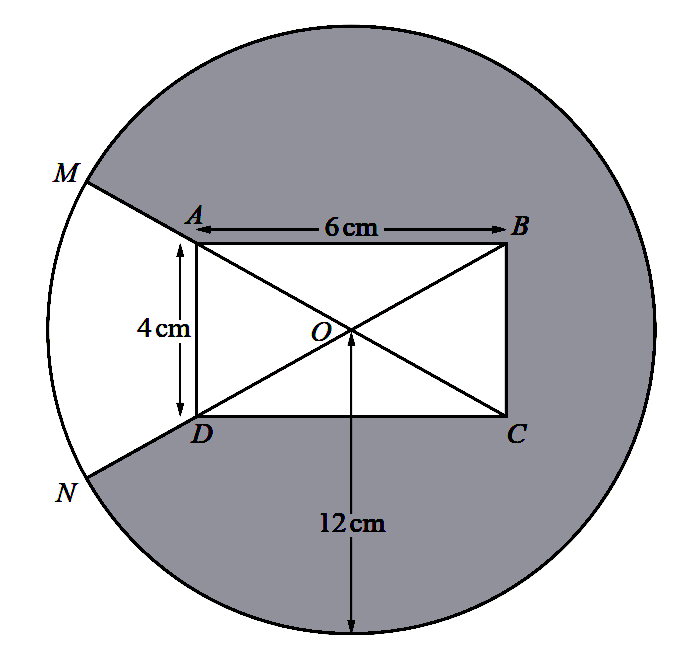
(a) Show that angle $A O D$ is $1.176$ radians correct to 3 decimal places.
[2]
(b) Find the perimeter of the shaded region.
[4]
(c) Find the area of the shaded region.
[3]
The diagram shows the graph of the curve $y=\dfrac{1}{(x+2)^{2}}+\dfrac{3}{(x+2)}$ for $x>-2$.
The points $A$ and $B$ lie on the curve such that the $x$-coordinates of $A$ and of $B$ are $-1$
and 2 respectively.
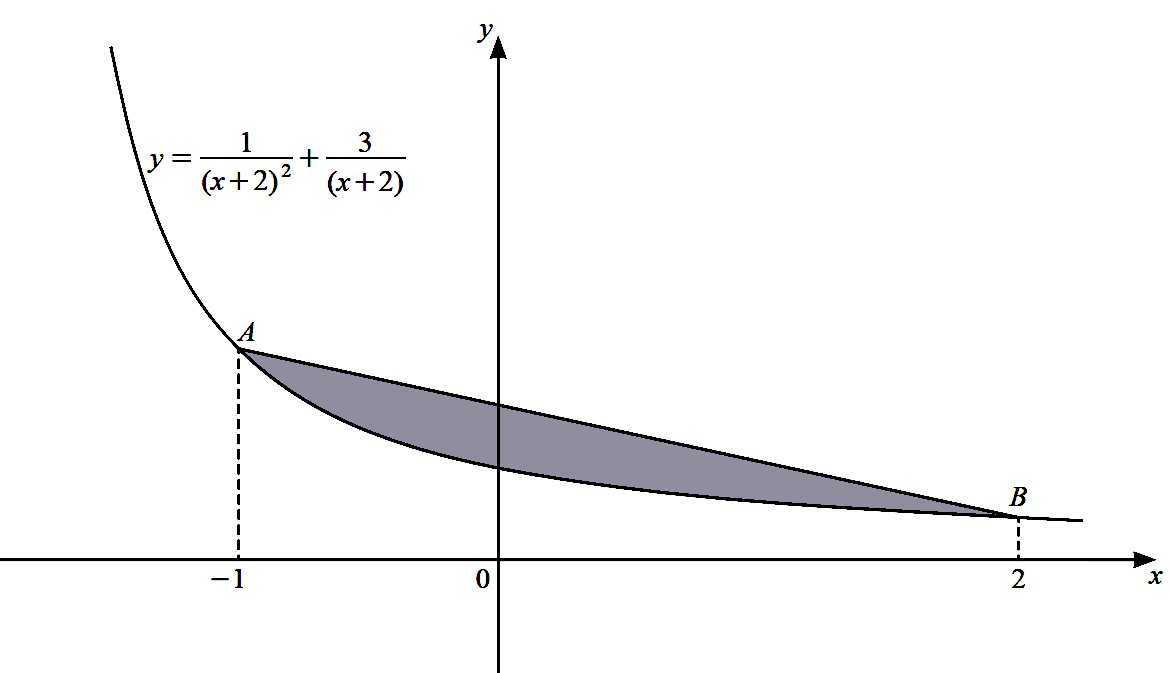
(a) Find the exact $y$-coordinates of $A$ and of $B$.
[2]
(b) Find the area of the shaded region enclosed by the line $A B$ and the curve,
giving your answer in the form $\dfrac{p}{q}-\ln r$, where $p, q$ and $r$ are
integers.
[6]
SOLUTION
(a) The set of the values of $x$ for which $f(x)< 0$ is $\{x \mid -3 < x < 1 \text{ or } x>5\}.\\\\ $
(b) Let $f(x)=a(x+3)(x-1)(x-5)$
When $x=0, f(x)=15 a\\\\ $
According to the diagram
$\begin{aligned}
&\\
15 a &=-5 \\\\
a &=-\frac{1}{3}\\\\
\therefore\ f(x) &=-\frac{1}{3}(x+3)(x-1)(x-5) \\\\
&=-\frac{1}{3}(x+3)\left(x^{2}-6 x+5\right) \\\\
&=-\frac{1}{3}\left(x^{3}-6 x^{2}+5 x+3 x^{2}-18 x+15\right) \\\\
&=-\frac{1}{3}\left(x^{3}-3 x^{2}-13 x+5\right)
\end{aligned}$
$\begin{aligned}
\text{ (a) }\quad \frac{\sqrt[3]{x y}(z y)^{2}}{(x z)^{-3} \sqrt{z}} &=\frac{x^{\frac{1}{3}} y^{\frac{1}{3}} z^{2} y^{2}}{x^{-3} z^{-3} z^{\frac{1}{2}}} \\\\
&=x^{\frac{1}{3}+3} y^{\frac{1}{3}+2} z^{2+3-\frac{1}{2}} \\\\
&=x^{\frac{10}{3}} y^{\frac{7}{3}} z^{\frac{9}{2}}\\\\
\frac{\sqrt[3]{x y}(z y)^{2}}{(x z)^{-3} \sqrt{z}} &=x^{a} y^{b} z^{c} \quad \text { (given) } \\\\
x^{\frac{10}{3} \frac{7}{3}} z^{\frac{9}{2}} &=x y^{b} z^{c} \\\\
\therefore \quad a &=\frac{10}{3} \\\\
b &=\frac{7}{3} \\\\
c &=\frac{9}{2}\\\\
\end{aligned}$
$\begin{aligned}
\text{ (b) }\quad 5\left(2^{2 p+1}\right)-17\left(2^{p}\right)+3 &= 0 \\\\
5\left(2 \times 2^{2 p}\right)-17\left(2^{p}\right)+3 &= 0 \\\\
10\left(2^{p}\right)^{2}-17\left(2^{p}\right)+3 &= 0 \\\\
\left(5 \times 2^{p}-1\right)\left(2 \times 2^{p}-3\right) &= 0 \\\\
2^{p} =\frac{1}{5} \text { or } 2^{p}& =\frac{3}{2} \\\\
p=\log_{2} \left(\frac{1}{5}\right) \text { or } p &=\log_{2} \left(\frac{3}{2}\right)\\\\
p=\frac{\ln \frac{1}{5}}{\ln 2} \quad \text { or } p&=\frac{\ln \frac{3}{2}}{\ln 2} \\\\
p=-2.32 \quad \text { or } p&=0.585
\end{aligned}
$
SOLUTION
$\begin{aligned}
\text{ (a) }\qquad & 3+2 \lg a-4 \lg b \\\\
=&\ \lg 10^{3}+\lg a^{2}-\lg b^{4} \\\\
=&\ \lg \frac{10^{3} a^{2}}{b^{4}}\\\\
\end{aligned}$
$\begin{aligned}
\text{ (b) } \hspace{1.5cm} 3 \log _{a} 4+2 \log a &=7 \\\\
\frac{3}{\log _{4} a}+2 \log a &=7 \\\\
3+2\left(\log _{4} a\right)^{2} &=7 \log _{4} a \\\\
2(\log_{4} a)^{2}-7 \log _{4} a+3 &=0 \\\\
(2 \log_{4} a-1)\left(\log _{4} a-3\right) &=0 \\\\
\log _{4} a =\frac{1}{2} \text { or } \log _{4} a &=3 \\\\
a =2 \text { or } a &=64
\end{aligned}$
SOLUTION
$\begin{aligned}
& \cot \left(2 x+\frac{\pi}{3}\right)-\sqrt{3}=0,-\pi<x<\pi\\\\
& \cot \left(2 x+\frac{\pi}{3}\right)=\sqrt{3}\\\\
& \tan \left(2 x+\frac{\pi}{3}\right)=\frac{1}{\sqrt{3}}\\\\
& 2 x+\frac{\pi}{3}=-\frac{5 \pi}{6} \text { or } 2 x+\frac{\pi}{3}=\frac{\pi}{6} \text { or }
2 x+\frac{\pi}{3}=\frac{7 \pi}{6} \text { or } 2 x+\frac{\pi}{3}=\frac{13 \pi}{6}\\\\
& x=-\frac{7 \pi}{12} \text { or } x=-\frac{\pi}{12} \text { or } x=\frac{5 \pi}{12} \text { or }
x=\frac{11 \pi}{12}
\end{aligned}$
SOLUTION
Curve: $y=5 \sin \frac{x}{3}+4\\\\ $
Since $y=c$ is tangent to the curve, $c$ must be either maximum or minimum value.
$\begin{aligned}
& \\
& -1 \leq \sin \frac{x}{3} \leq 1\\\\
& -5 \leq 5 \sin \frac{x}{3} \leq 5\\\\
& -5+4 \leq 5 \sin \frac{x}{3}+4 \leq 5+4\\\\
& -1 \leq y \leq 9\\\\
\therefore\ & c=-1\ \text{ or }\ c=9.
\end{aligned}$
SOLUTION
$p(x)=10 x^{3}+a x^{2}-10 x+b\\\\ $
$p(x)$ is divisible by $2 x+1$.
$\begin{aligned}
&\\
\therefore\ & p\left(-\frac{1}{2}\right)=0 \\\\
&10\left(-\frac{1}{2}\right)^{3}+a\left(-\frac{1}{2}\right)^{2}-10\left(-\frac{1}{2}\right)+b=0 \\\\
&-\frac{5}{4}+\frac{a}{4}+5+b=0 \\\\
&-5+a+20+4 b=0 \\\\
\therefore\ & a+4 b=-15 \ldots(1)\\\\
\end{aligned}$
When $p(x)$ is divided by $(x+1)$, the remainder $=-24$
$\begin{aligned}
&\\
\therefore\ & p(-1)=-24 \\\\
& 10(-1)^{3}+a(-1)^{2}-10(-1)+b=-24 \\\\
&-10+a+10+b=-24 \\\\
\therefore\ & a+b=-24 \ldots(2)\\\\
\end{aligned}$
Subtracting equation (2) from equation (1),
$\begin{aligned}
&\\
3 b=9\\\\
b=3\\\\
\end{aligned}$
Substituting $b=3$ in equation (2),
$\begin{aligned}
&\\
& a+3=-24 \\\\
& a=-27 \\\\
\therefore\ & p(x)=10 x^{3}-27 x^{2}-10 x+3 \\\\
& \text { Let } p(x)=(2 x+1)\left(5 x^{2}+c x+3\right) . \\\\
\therefore\ &(2 x+1)\left(5 x^{2}+c x+3\right)=10 x^{3}-27 x^{2}-10 x+3 \\\\
& \text { When } x=1, \quad 3(8+c)=10-27-10+3
\end{aligned}$
SOLUTION
$\begin{aligned}
\text{(a) (i)} \hspace{1.5cm} \overrightarrow{A B} &=\overrightarrow{O B}-\overrightarrow{O A} \\\\
&=\vec{b}-\vec{a} \\\\
\text{(ii)} \hspace{1.5cm} \overrightarrow{B C} &=\overrightarrow{O C}-\overrightarrow{O B} \\\\
&=\vec{c}-\vec{b} \\\\
\text{(iii)} \quad AB: B C &=m: n \\\\
\therefore\ n \overrightarrow{A B} &=m \overrightarrow{B C} \\\\
n(\vec{b}-\vec{a}) &=m(\vec{c}-\vec{b}) \\\\
n \vec{b}-n \vec{a} &=m \vec{c}-m \vec{b} \\\\
\therefore\ \vec{b}+m \vec{b} &=n \vec{a}+m \vec{c} \\\\
n \vec{a}+m \vec{c} &=(m+n) \vec{b}\\\\
\end{aligned}$
$\begin{aligned}
\text{(b)} \quad \lambda\left(\begin{array}{l}
2 \\\\
1
\end{array}\right)+(\mu-1)\left(\begin{array}{r}
-4 \\\\
7
\end{array}\right) &=(\lambda+1)\left(\begin{array}{r}
4 \\\\
-2
\end{array}\right) \\\\
(\mu-1)\left(\begin{array}{r}
-4 \\\\
7
\end{array}\right) &=(\lambda+1)\left(\begin{array}{r}
4 \\\\
-2
\end{array}\right)-\lambda\left(\begin{array}{l}
2 \\\\
1
\end{array}\right) \\\\
\left(\begin{array}{l}
4-4 \mu \\\\
7 \mu-7
\end{array}\right) &=\left(\begin{array}{r}
4 \lambda+4 \\\\
-2 \lambda-2
\end{array}\right)-\left(\begin{array}{l}
2 \lambda \\\\
\lambda
\end{array}\right) \\\\
\left(\begin{array}{r}
4-4 \mu \\\\
7 \mu-7
\end{array}\right) &=\left(\begin{array}{r}
2 \lambda+4 \\\\
-3 \lambda-2
\end{array}\right) \\\\
4-4 \mu &=2 \lambda+4 \\\\
\lambda &=-2 \mu\\\\
7 \mu-7 &=-3 \lambda-2 \\\\
7 \mu-7 &=-3(-2 \mu)-2 \\\\
\mu &=5 \\\\
\therefore\ \lambda &=-10
\end{aligned}$
SOLUTION
$\text{ (a) }\ $ For $5$-digit even numbers greater than $50, 000$,
$\qquad $ If the leading digit is $5,7$ or $9$, the unit's digit must be $0, 4$ or $6$.
$\quad\therefore\ $ Number of ways $=3 \times{ }^{5} P_{3} \times 3=540$ ways.
$\qquad$ If the leading digit is $6$ , the units digit mult be $0$ or $4$.
$\quad\therefore\ $ Number of ways $=1 \times{ }^{5}P_{3} \times 2=120$ ways.
$\quad\therefore\ $ Total ways $=540+120=660$ ways.
$\begin{aligned}
&\\
\text{ (b) } \hspace{2.5cm} {}^nC_{4} &= 6 \times {}^nC_{2} \\\\
\frac{n !}{4 !(n-4) !} &=6 \times \frac{n !}{2 !(n-2) !} \\\\
\frac{1}{4 \times 3 \times 2 !(n-4) !} &=\frac{6}{2 !(n-2)(n-3)(n-4) !} \\\\
\frac{1}{12} &=\frac{6}{(n-2)(n-3)} \\\\
(n-2)(n-3) &=72 \\\\
(n-2)(n-3) &=9 \times 8 \\\\
(n-2)(n-3) &=(11-2)(11-3) \\\\
\therefore\ n &=11
\end{aligned}$
SOLUTION
$\begin{aligned}
\text { radius } &=12 \mathrm{~cm} \\\\
\therefore O M&=O N =12 \mathrm{~cm} \\\\
A C &=\sqrt{6^{2}+4^{2}} \\\\
&=\sqrt{36+16} \\\\
&=2 \sqrt{13} \mathrm{~cm} \\\\
\therefore O A&=O B=O C =O D=\sqrt{13} \mathrm{cu} \\\\
&=\cos ^{-1} \frac{O A^{2}+O D^{2}-A D^{2}}{2.0 A \cdot O D} \\\\
&=\cos ^{-1} \frac{13+13-16}{2(\sqrt{13})(\sqrt{13})} \\\\
&=1.176 \text{rad}\\\\
\end{aligned}$
$\quad $ arc length of major arc $MN$
$\begin{aligned}
&\\
s&=12 \times(2 \pi-1.176) \mathrm{cm} \\\\
M A&=N D=12-\sqrt{13} \mathrm{~cm}\\\\
\end{aligned}$
$\therefore$ perimeter of shaded region
$\begin{aligned}
&\\
&=m A+N D+A B+C D+B C+S \\\\
&=12-\sqrt{13}+12-\sqrt{13}+6+6+4+12(2 \pi-1.176) \\\\
&=94.1 \mathrm{~cm}\\\\
\end{aligned}$
$\begin{aligned}
&\quad\text { area of major sector } MN \\\\
&=\frac{1}{2} r s \\\\
&=\frac{1}{2} \times 12 \times 12(2 \pi-1.176) \\\\
&=367.72 \mathrm{~cm}^{2} \\\\
&\quad\text { area of rectangle } ABCD \\\\
&=6 \times 4 \\\\
&=24 \mathrm{~cm}^{2}\\\\
&\quad\text { area of } \triangle A O D\\\\
&=\frac{1}{2} \times O A \times O D \times \sin (\angle A O D) \\\\
&=\frac{1}{2} \times 13 \sin (1.176) \\\\
&=6\\\\
\end{aligned}$
$\begin{aligned}
&\quad\text{area of shaded region }\\\\
&=\text{area of major sector } - \text{ area of rectangle } + \text{area of triangle }\\\\
&=367.72-24+6 \\\\
&=349.72 \mathrm{~cm}^{2}
\end{aligned}$
$\begin{aligned}
\text{ Curve } : y&=\dfrac{1}{(x+2)^{2}}+\dfrac{3}{(x+2)}\\\\
\text{ When } x&=-1,\\\\
y &=\dfrac{1}{(-1+2)^{2}}+\dfrac{3}{(-1+2)} \\\\
&=4\\\\
\text{ When } x&=2,\\\\
y &=\dfrac{1}{(2+2)^{2}}+\dfrac{3}{(2+2)} \\\\
&=\dfrac{13}{16}\\\\
\end{aligned}$
$\therefore$ The points $A$ and $B$ respectively are $(-1,4)$ and $\left(2, \dfrac{13}{16}\right).\\\\ $
The equation of the line passing through $A$ and $B$ is
$\begin{aligned}
&\\
y-4 &=\dfrac{\dfrac{13}{16}-4}{2-(-1)}(x+1) \\\\
y-4 &=-\dfrac{17}{16}(x+1) \\\\
y &=-\dfrac{17}{16}(x+1)+4\\\\
&\qquad\text{ area of shaded region }\\\\
&=\int_{-1}^{2}\left[-\dfrac{17}{16}(x+1)+4-\dfrac{1}{(x+2)^{2}}-\dfrac{3}{x+2}\right] d x \\\\
&=\int_{-1}^{2}\left[-\dfrac{17}{16} x-\dfrac{17}{16}+4-(x+2)^{-2}-\dfrac{3}{x+2}\right] d x \\\\
&=\int_{-1}^{2}\left[-\dfrac{17}{16} x+\dfrac{47}{16}-(x+2)^{-2}-\dfrac{3}{x+2}\right] d x \\\\
&=\left[-\dfrac{17}{32} x^{2}+\dfrac{47}{16} x+\dfrac{1}{x+2}-3 \ln (x+2)\right]_{-1}^{2}\\\\
&=\left(-\dfrac{17}{32} \times 4+\dfrac{47}{16} \times 2+\dfrac{1}{4}-3 \ln 4\right)-\left(-\dfrac{17}{32}-\dfrac{47}{16}+1-3 \ln 1\right) \\\\
&=-\dfrac{17}{8}+\dfrac{47}{8}+\dfrac{2}{8}-3 \ln 4+\dfrac{17}{32}+\dfrac{47}{16}+1+3 \ln 1 \\\\
&=\dfrac{207}{32}-3(\ln 4-\ln 1) \\\\
&=\dfrac{207}{32}-3 \ln \dfrac{4}{1}\\\\
&=\dfrac{207}{32}-\ln 64\\\\
\end{aligned}$

Post a Comment for "Oct-Nov-21-p1-CIE-4037-12 : Solution"