May-June-21-CIE-9709-11 : AS and A Level - Problems and Solutions
2021 (May-June) CIE (9709-Pure Mathematics 1), Paper 1/11 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။
The equation of a curve is such that $\dfrac{d y}{d x}=\dfrac{3}{x^{4}}+32 x^{3}$.
It is given that the curve passes through the point $\left(\dfrac{1}{2}, 4\right)$.
Find the equation of the curve.
[4]
The sum of the first $20$ terms of an arithmetic progression is $405$ and the sum of
the first $40$ terms is $1410$ .Find the $60^{\text{th}}$ term of the progression.
[5]
SOLUTION
(a) Find the first three terms in the expansion of $(3 - 2x)^5$ in ascending powers
of $x$.
[3]
(b) Hence find the coefficient of $x^2$ in the expansion of $(4 + x)^2(3-2x)^5$.[3]
[4]
SOLUTION
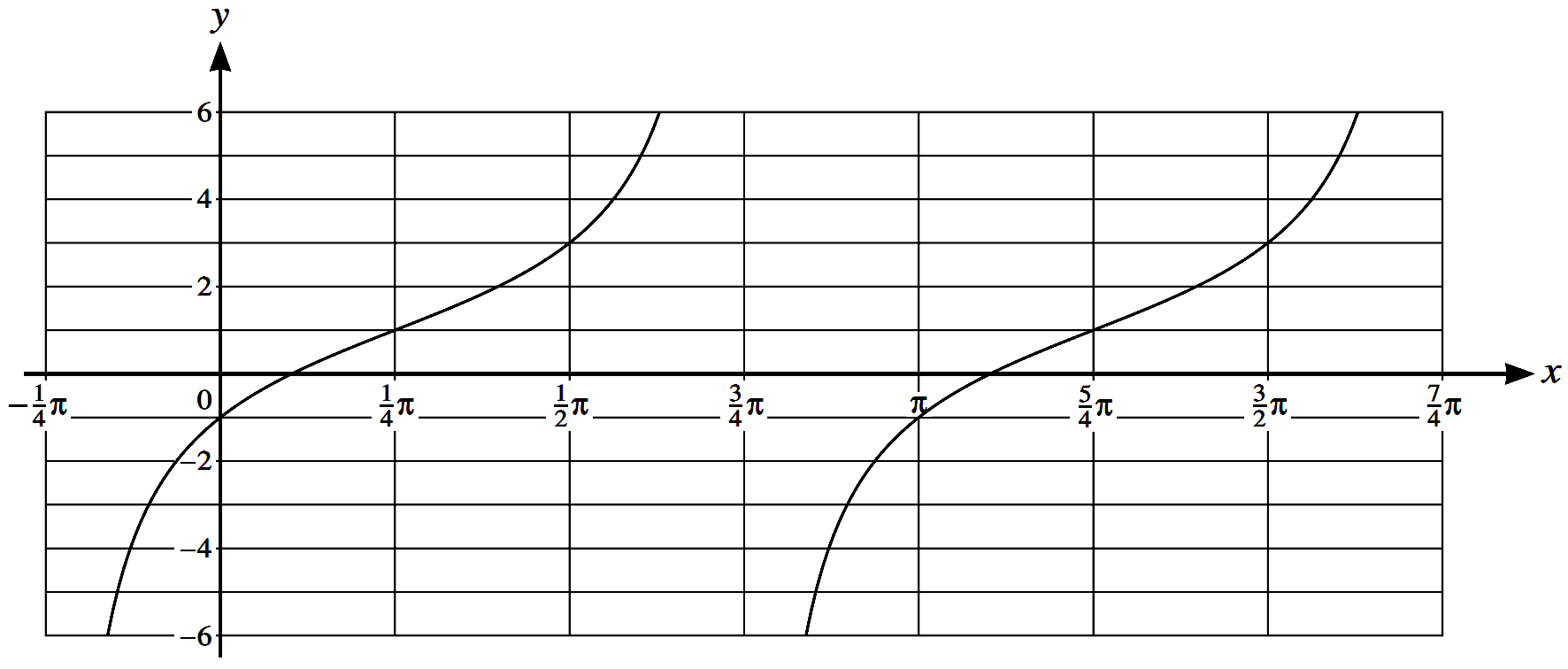
The diagram shows part of the graph of $y = a \tan (x - b) + c$.
Given that $0 < b < \pi$, state the values of the constants $a, b$ and $c$.
[4]
The fifth, sixth and seventh terms of a geometric progression are $8k$, $-12$ and
$2k$ respectively.Given that $k$ is negative, find the sum to infinity of
the progression.
[4]
SOLUTION
The equation of a curve is $y = (2k - 3)x^2 - kx - (k - 2)$, where $k$ is a constant.
The line $y = 3x - 4$ is a tangent to the curve. Find the value of $k$.
[5]
(a) Prove the identity $\dfrac{1-2 \sin ^{2} \theta}{1-\sin ^{2} \theta} \equiv 1-\tan ^{2} \theta$.
[2]
(b) Hence solve the equation
$\dfrac{1-2 \sin ^{2} \theta}{1-\sin ^{2} \theta}=2 \tan ^{4} \theta$ for $0^{\circ} \leq \theta \leq 180^{\circ}$.
[3]
SOLUTION
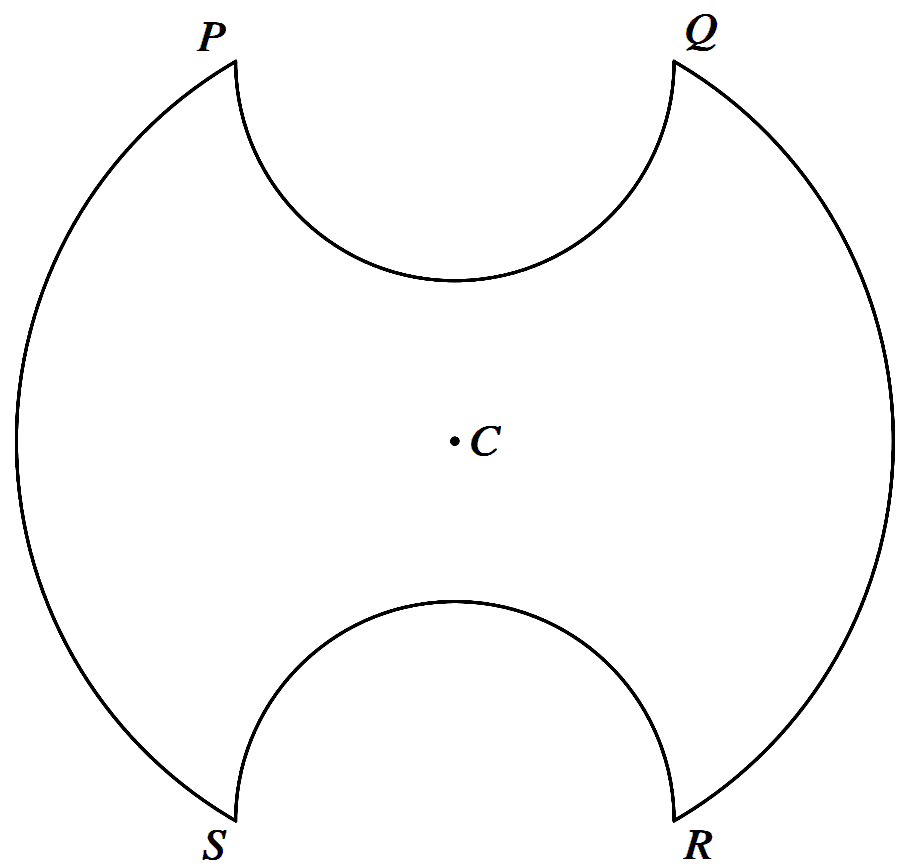
The diagram shows a symmetrical metal plate. The plate is made by removing two identical
piecesfrom a circular disc with centre $C$. The boundary of the plate consists of two
arcs $PS$ and $QR$ of the original circle and two semicircles with $PQ$ and $RS$ as diameters.
The radius of the circle with centre
$C$ is $4$ cm, and $PQ = RS = 4$ cm also.
(a) Show that angle $PCS = \dfrac{2}{3}\pi$ radians.
[2]
(b) Find the exact perimeter of the plate.
[3]
(c) Show that the area of the plate is $\left(\dfrac{20}{3} \pi+8 \sqrt{3}\right) \mathrm{cm}^{2}$.
[5]
SOLUTION
Functions $f$ and $g$ are defined as follows:
$\begin{aligned}
&\\
&f(x)=(x-2)^{2}-4 \text { for } x \geq 2 \\\\
&g(x)=a x+2 \text { for } x \in \mathbb{R}\\\\
\end{aligned}$
where $a$ is a constant.
(a) State the range of $f$.
[1]
(b) Find $f^{-1}(x)$.
[2]
(c) Given that $a = -\dfrac{5}{3}$, solve the equation $f(x) = g(x)$.
[3]
(d) Given instead that $ggf^{-1}(12) = 62$, find the possible values of $a$.
[5]
SOLUTION
The equation of a circle is $x^2 + y^2 - 4x + 6y - 77 = 0$.
(a) Find the $x$-coordinates of the points $A$ and $B$ where the circle
intersects the $x$-axis.
[2]
(b) Find the point of intersection of the tangents to the circle at $A$ and $B$.
[6]
SOLUTION
The equation of a curve is $y=2 \sqrt{3 x+4}-x$.
(a) Find the equation of the normal to the curve at the point $(4,4)$,
giving your answer in the form $y=m x+c$.
[5]
(b) Find the coordinates of the stationary point.
[3]
(c) Determine the nature of the stationary point.
[2]
(d) Find the exact area of the region bounded by the curve,
the x-axis and the lines $x = 0$ and $x = 4$.
[4]
SOLUTION
$\begin{aligned}
\frac{d y}{d x} &=\frac{3}{x^{4}}+32 x^{3} \\\\
y &=\int\left(\frac{3}{x^{4}}+32 x^{3}\right) d x \\\\
&=3 \int x^{-4} d x+32 \int x^{3} d x \\\\
&=-\frac{1}{x^{3}}+8 x^{4}+C\\\\
\end{aligned}$
The curve passes through the point $\left(\dfrac{1}{2}, 4\right)$.
$\begin{aligned}
&\\
\therefore\ 4&=-\frac{1}{\left(\frac{1}{2}\right)^{3}}+8\left(\frac{1}{2}\right)^{4}+c \\\\
&4=-8+\frac{1}{2}+c \\\\
&c=\frac{23}{2} \\\\
&y=-\frac{1}{x^{3}}+8 x^{4}+\frac{23}{2}
\end{aligned}$
Let the first term be $a$, the common difference be $d$ and
the sum to first $n$ terms be $S_n$ of given A.P.
$\begin{aligned}
&\\
\therefore\ S_{20} &=405 \\\\
\frac{20}{2}\{2 a+19 d\} &=405 \\\\
2 a+19 d &=40.5 \ldots (1)\\\\
S_{40} &=1410 \\\\
\frac{40}{2}\{2 a+39 d\} &=1410 \\\\
2 a+39 d &=70.5 \ldots (2)\\\\
\end{aligned}$
Solving equation $(1)$ and (2),
$\begin{aligned}
&\\
a=6, d &=\frac{3}{2} \\\\
\therefore\ 60^{\text {th }} \text { term } &=a+59 d \\\\
&=6+59 \times \frac{3}{2} \\\\
&=94.5
\end{aligned}$
$\begin{aligned}
(3-2 x)^{5}&=3^{5} 5\left(3^{4}\right)(2 x)+10\left(3^{3}\right)(2 \times)^{2}+\cdots \\\\
&=24^{3}-810 x+1080 x^{2}+\cdots \\\\
(4+x)^{2}&=16+8 x+x^{2} \\\\
(4+x)^{2}(3+2 x)^{5}&=\left(16+8 x+x^{2}\right)\left(2 y^{3}-810 x+1080 x^{2}+\cdots\right) \\\\
\therefore & \quad\text { Coefficient of } x^{2} \text { in the expansion of }(4+x)^{2}(3+2 x)^{5} \\\\
&=16(1080)-8(80)+1(243) \\\\
&=11043
\end{aligned}$
SOLUTION
$y=a \tan (x-b)+c\\\\ $
The graph passes throught the points $(0,-1),\left(\dfrac{\pi}{4},+\right)$ and
$\left(\dfrac{\pi}{2}, 3\right)$.
$\begin{aligned}
&\\
&a \tan (0-b)+c=-1\\\\
&-a \tan b+c=-1 \ldots (1)\\\\
&a \tan \left(\frac{\pi}{4}-b\right)+c=1 \ldots(2)\\\\
&a \tan \left(\frac{\pi}{2}-b\right)+c=3 \ldots(3)\\\\
&(2)-(1)\\\\
&a\left[\tan \left(\frac{\pi}{4}-b\right)+\tan b\right]=2\\\\
&(3)-(2), \\\\
&a\left[\tan \left(\frac{\pi}{2}-b\right)-\tan \left(\frac{\pi}{4}-b\right)\right]=2\\\\
&\therefore\ \tan \left(\frac{\pi}{4}-b\right)+\tan b=\tan \left(\frac{\pi}{2}-b\right)-\tan \left(\frac{\pi}{4}-b\right)\\\\
&\tan \left(\frac{\pi}{4}-b\right) =\frac{1}{2}\left[\tan \left(\frac{\pi}{2}-b\right)-\tan b\right] \\\\
&\frac{1-\tan b}{1+\tan b} =\frac{1}{2}\left[\frac{1}{\tan b}-\tan b\right] \\\\
&\frac{1-\tan b}{1+\tan b} =\frac{1-\tan ^{2} b}{2 \tan b}\\\\
&2 \tan b-2 \tan ^{2} b =1-\tan ^{2} b+\tan b-\tan ^{3} b\\\\
&\tan ^{3} b-\tan ^{2} b+\tan b-1=0 \\\\
&\tan ^{2} b(\tan b-1)+\tan b-1=0\\\\
&(\tan b-1)\left(\tan ^{2} b+1\right)=0\\\\
&\text{ For } 0 < b<\pi, \tan ^{2} b+1>0\\\\
&\therefore \ \tan b-1=0\\\\
&\tan b=1\\\\
&b=\frac{\pi}{4}\\\\
\end{aligned}$
Substituting $b=\dfrac{\pi}{4}$ in equation $(2),c=1\\\\\\\\ $
Substituting b $=\dfrac{\pi}{4}$ and $c=1$ in equation $(1)$,
$\begin{aligned}
&\\
&-a \tan \frac{\pi}{4}+1 =-1 \\\\
&-a+1 =-1 \\\\
&a =2
\end{aligned}$
$\begin{aligned}
\text{In a G . P,}& \\\\
u_{5} & =8 k \\\\
u_{6} & =-12 \\\\
u_{7} & =2 k \\\\
\therefore\ \frac{-12}{8 k} & =\frac{2 k}{-12} \\\\
k^{2} & =9 \\\\
k & =-3(\because k<0)\\\\
\therefore\ u_{5} & =-24 \\\\
u_{6} &=-12 \\\\
u_{7} &=-6 \\\\
r &=\frac{-6}{-12} \\\\
&=\frac{1}{2} \\\\
a r &=-24 \\\\
a\left(\frac{1}{2}\right)^{4} &=-24\\\\
a&=-384\\\\
\end{aligned}$
Let the sum to infinity be $S$, then
$\begin{aligned}
&\\
S &=\frac{a}{1-r} \\\\
&=\frac{-384}{1-\frac{1}{2}} \\\\
&=-768
\end{aligned}$
SOLUTION
$\begin{aligned}
\text{ Curve }: y&=(2 k-3) x^{2}-k x-(k-2)\\\\
\text{ Line }: y&=3 x-4\\\\
\end{aligned}$
At the point of intersection line and curve,
$\begin{aligned}
&(2 k-3) x^{2}-k x-(k-2)=3 x-4 \\\\
\therefore\ &(2 k-3) x^{2}-(k+3) x+6-k=0\\\\
\end{aligned}$
Since the line is tangent to the curve,
$\begin{aligned}
&\\
&\text{ Discriminant } =0\\\\
&(k+3)^{2}-4(2 k-3)(6-k)=0\\\\
&k^{2}+6 k+9-4\left(-2 k^{2}+15 k-18\right)=0 \\\\
&k^{2}+6 k+9+8 k^{2}-60 k+72=0 \\\\
&9 k^{2}-54 k+81=0 \\\\
&k^{2}-6 k+9=0 \\\\
&(k-3)^{2}=0 \\\\
&k=3
\end{aligned}$
$\begin{aligned}
\dfrac{1-2 \sin ^{2} \theta}{1-\sin ^{2} \theta} &=\dfrac{\cos ^{2} \theta-\sin ^{2} \theta}{\cos ^{2} \theta} \\\\
&=\dfrac{\cos ^{2} \theta}{\cos ^{2} \theta}-\dfrac{\sin ^{2} \theta}{\cos ^{2} \theta} \\\\
&=1-\tan ^{2} \theta\\\\
\end{aligned}$
$\begin{aligned}
&\dfrac{1-2 \sin ^{2} \theta}{1-\sin ^{2} \theta}=2 \tan ^{4} \theta \\\\
&1-\tan ^{2} \theta=2 \tan ^{4} \theta \\\\
&2 \tan ^{4} \theta+\tan ^{2} \theta-1=0 \\\\
&\left(2 \tan ^{2} \theta-1\right)\left(\tan ^{2} \theta+1\right)=0 \\\\
&\sin \cot \tan ^{2} \theta+1>0 \\\\
& 2 \tan ^{2} \theta-1=0 \\\\
&\tan ^{2} \theta=\dfrac{1}{2} \\\\
&\tan \theta=-\dfrac{1}{\sqrt{2}} \text { or } \tan \theta=\dfrac{1}{\sqrt{2}} \\\\
&\theta=144.7^{\circ} \text { or } \theta=35.3^{\circ}
\end{aligned}$
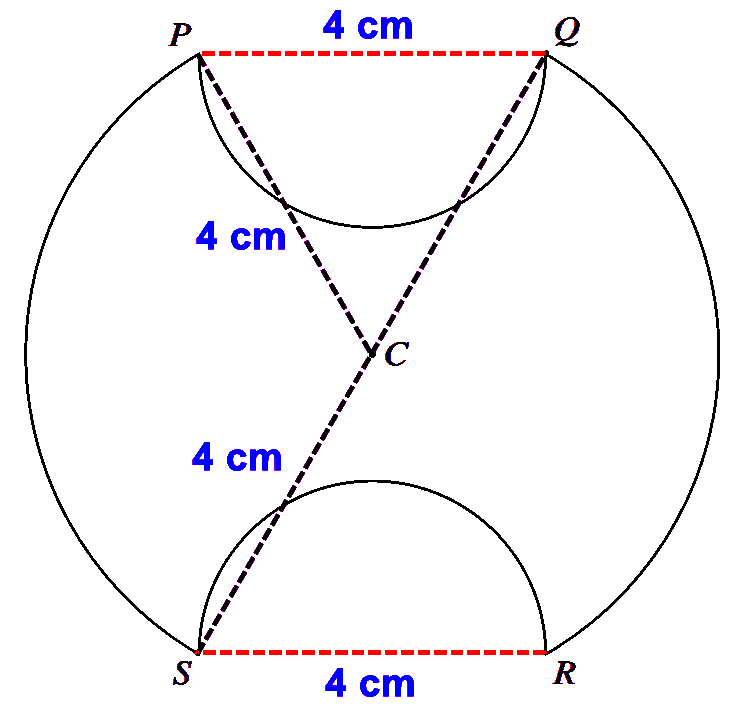
$\text{ (a) } \quad \triangle P C Q$ is equilateral.
$\begin{aligned}
&\\
\therefore \quad \angle P C Q &=\frac{\pi}{3} \\\\
\angle P C S &=\pi-\frac{\pi}{3} \\\\
&=\frac{2 \pi}{3} \\\\
\end{aligned}$
$\begin{aligned}
\text{ (b) } \quad & \qquad \text{ arc length of } PS \\\\
&= \text{ arc length of } SR \\\\
&= 4 \times \frac{2 \pi}{3} \\\\
&= \frac{8 \pi}{3} \mathrm{~cm}\\\\
\end{aligned}$
$\begin{aligned}
&\quad \text{ arc length of semicircle } PQ \\\\
&= \text{ arc length of semicircle } SR\\\\
&=\pi \times \frac{4}{2} \\\\
&=2 \pi\ \mathrm{cm}\\\\
&\quad \text{ perimeter of metal plate }\\\\
&=2\left(\frac{8 \pi}{3}+2 \pi\right) \\\\
&=\frac{28 \pi}{3} \mathrm{~cm}\\\\
\end{aligned}$
$\begin{aligned}
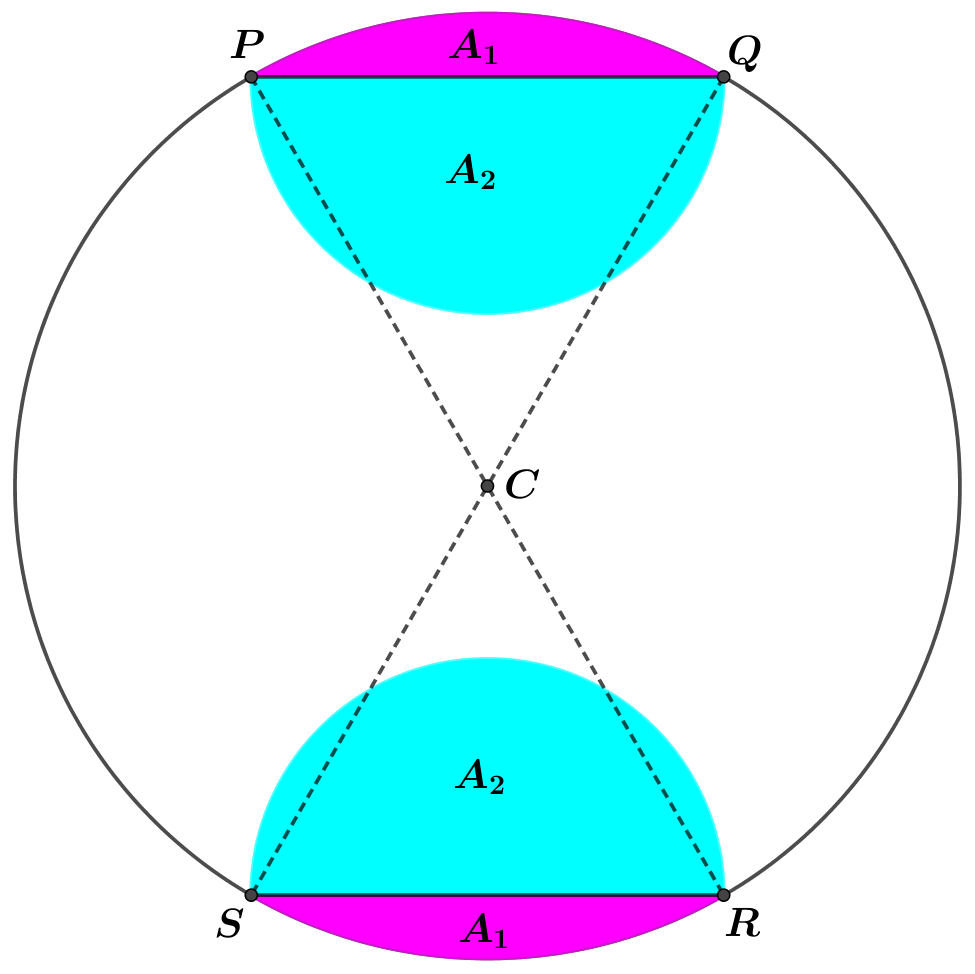
\text{ (c) } \quad A_{1} &= \text{ area of sector - area of triangle}\\\\
&=\frac{1}{2} \times 4^{2} \times \frac{\pi}{3}-\frac{\sqrt{3}}{4} \times 4^{2} \\\\
&=\frac{8 \pi}{3}-4 \sqrt{3} \\\\
A_{2} &=\text { area of semicircle } \\\\
&=2 \pi\\\\
&\quad\text{ area of metal plate }\\\\
&=\text { area of } \odot C-2\left(A_{1}+A_{2}\right) \\\\
&=\pi \times 4^{2}-2\left(\frac{8 \pi}{3}-4 \sqrt{3}+2 \pi\right) \\\\
&=\left(\frac{20 \pi}{3}+8 \sqrt{3}\right) \mathrm{cm}^{2}
\end{aligned}$
$ \begin{aligned}
f(x)=(x-2)^{2}-4 , x \geq 2\\\\
g(x)=a x+2, x \in R\\\\
\end{aligned}$
$\text{ (a) }\ $ range of $f=\{y \mid y \geq-4, y \in R\}$
$\begin{aligned}
&\\
\text{ (b) } \text{ Let } f^{-1}(x)&=y\\\\
f(y) &=x \\\\
(y-2)^{2}-4 &=x \\\\
(y-2)^{2} &=x+4 \\\\
y &=\pm \sqrt{x+4}+2\\\\
\end{aligned}$
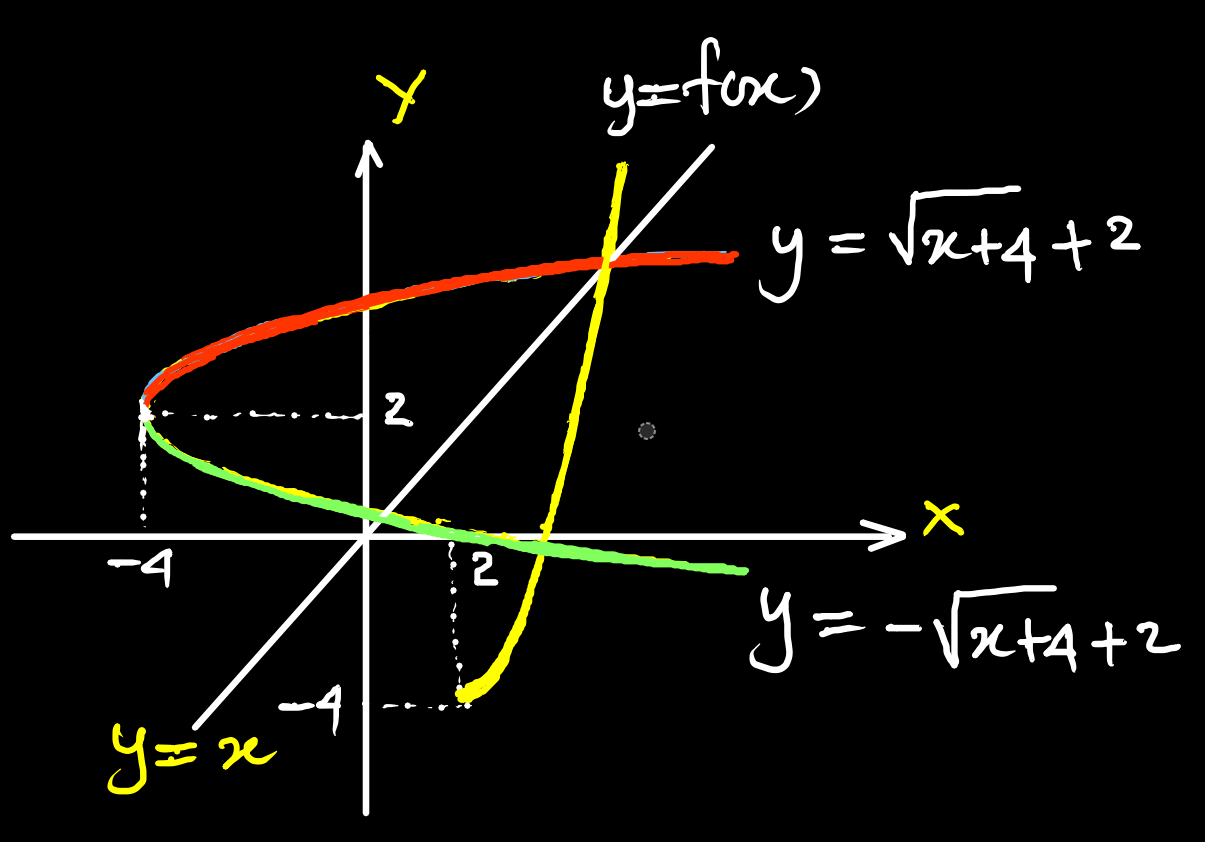
Since $f^{-1}(x)$ is the reflection of $f(x)$ in the line $y=x$, $f^{-1}(x)=\sqrt{x+4}+2$.
$\begin{aligned}
&\\
\text{ (c) }\hspace{1cm}\text { When } a &=-\frac{5}{3},\\\\
g(x) &=-\frac{5}{3} x+2 \\\\
f(x) &=g(x) \\\\
(x-2)^{2}-4 &=-\frac{5}{3} x+2 \\\\
x^{2}-4 x &=-\frac{5}{3} x+2 \\\\
3 x^{2}-12 x &=-5 x+6 \\\\
3 x^{2}-7 x-6 &=0 \\\\
(3 x+2)(x-3) &=0 \\\\
x=-\frac{2}{3} \text { or } x &=3\\\\
\end{aligned}$
$\begin{aligned}
\text{ (d) }\hspace{1cm} g g f^{-1}(12) &=62 \\\\
g\left(g\left(f^{-1}(12)\right)\right) &=62 \\\\
g(g(\sqrt{12+4}+2)) &=62 \\\\
g(g(6)) &=62 \\\\
g(6 a+2) &=62 \\\\
a(6 a+2)+2 &=62 \\\\
6 a^{2}+2 a-60 &=0 \\\\
3 a^{2}+a-30 &=0 \\\\
(3 a+10)(a-3) &=0\\\\
\therefore\ a=-\frac{10}{3} \text { or } a &=3
\end{aligned}$
$\begin{aligned}
& x^{2}+y^{2}-4 x+6 y-77=0 \\\\
& x^{2}+y^{2}-4 x+6 y=77 \\\\
& x^{2}-4 x+4+y^{2}+6 y+9=77+13 \\\\
&(x-2)^{2}+(y+3)^{2}=90\\\\
\end{aligned}$
Let $O$ be the centere of tre circle.
$\therefore$ The coordinates of the point $O$ is $(2,-3)\\\\ $.
When the circle interseets $x$-axis, $y=0\\\\ $.
$\begin{aligned}
&\\
\therefore\ &(x-2)^{2}+9=90 \\\\
&(x-2)^{2}=81 \\\\
& x-2=\pm 9 \\\\
\therefore\ & x=2-9 \text { or } x=2+9 \\\\
\therefore\ & x=-7 \text { or } x=11\\\\
\end{aligned}$
$\therefore$ The circle intersects $x$-axis at $A(-7,0)$ and $B(11, 0).\\\\ $
Gradient of $A O=\dfrac{-3}{2+7}=-\dfrac{1}{3}\\\\ $
$\therefore$ Gradient of tangent at $A=3\\\\ $
Equation of tangent at $A$ is $y=3(x+7)\\\\ $
Gradient of $B O=\dfrac{-3}{2-11}=\dfrac{1}{3}\\\\ $
Gradient of tangent at $B=-3.\\\\ $
Equation of tangent at $B$ is $y=-3(x-11)\\\\ $
At the point of intersection of two tangents,
$\begin{aligned}
&\\
3(x+7) &=-3(x-11) \\\\
x+7 &=-x+11 \\\\
x &=2 \\\\
\therefore\ y &=27\\\\
\end{aligned}$
$\therefore\ $ The point of intersection of the two tangents is $(2,27).$
SOLUTION
$\text{ (a) }$ Curve: $y=2 \sqrt{3 x+4}-x$
$\begin{aligned}
&\\
\dfrac{d y}{d x} &=\dfrac{2}{2 \sqrt{3 x+4}} \dfrac{d}{d x}(3 x+4)-1 \\\\
&=\dfrac{3}{\sqrt{3 x+4}}-1
\end{aligned}$
At the point $(4,4)$,
$\begin{aligned}
&\\
\dfrac{d y}{d x} &=\dfrac{3}{\sqrt{12+4}}-1 \\\\
&=\dfrac{3}{4}-1=-\dfrac{1}{4}\\\\
\end{aligned}$
$\therefore$ Gradient of normal at $(4,4)$ is 4.
Equation of normal to the curve at $(4,4)$ is
$\begin{aligned}
&\\
y-4 &=4(x-4) \\\\
y &=4 x-12\\\\
\text{ (b) } \quad \text{ When } \dfrac{d y}{d x}&=0\\\\
\dfrac{3}{\sqrt{3 x+4}}-1&=0\\\\
\sqrt{3 x+4} &=3 \\\\
3 x+4 &=9 \\\\
x &=\dfrac{5}{3} \\\\
\text { When } x &=\dfrac{5}{3} \\\\
y &=2 \sqrt{3\left(\dfrac{5}{3}\right)+4}-\dfrac{5}{3} \\\\
&=\dfrac{13}{3}\\\\
\end{aligned}$
$\therefore$ The stationary point is $\left(\dfrac{5}{3}, \dfrac{13}{3}\right)$.
$\begin{aligned}
&\\
\text{ (c) } \quad \dfrac{d^{2} y}{d x^{2}} &=\dfrac{d}{d x}\left(\dfrac{3}{\sqrt{3 x+4}}-1\right) \\\\
&=\dfrac{d}{d x}\left(3(3 x+4)^{-1/2}-1\right) \\\\
&=-\dfrac{9}{2(3 x+4)^{3 / 2}}\\\\
\text { When } x&=\dfrac{5}{3}\\\\
\dfrac{d^{2} y}{d x^{2}}&=\dfrac{-9}{2 \sqrt{3\left(\dfrac{5}{3}\right)+4}}<0\\\\
\end{aligned}$
$\therefore\left(\dfrac{5}{3}, \dfrac{13}{3}\right)$ is a maximum.
$\begin{aligned}
&\\
\text{ (d) }\quad\text { required area } &=\displaystyle\int_{0}^{4}\left[2(3 x+4)^{1/2}-x\right] d x \\\\
&=2 \displaystyle\int_{0}^{4}(3 x+4)^{1 / 2} d x-\displaystyle\int_{0}^{4} x d x \\\\
&=\dfrac{2}{3} \displaystyle\int_{0}^{4}(3 x+4)^{1/2} d(3 x+4)-\displaystyle\int_{0}^{4} x d x \\\\
&\left.=\dfrac{4}{9}\left[(3 x+4)^{3 / 2}\right]_{0}^{4}-\dfrac{x^{2}}{2}\right]_{0}^{4} \\\\
&=\dfrac{4}{9}[64-8]-\dfrac{16}{2}\\\\
&=\dfrac{152}{9}
\end{aligned}$

Post a Comment for "May-June-21-CIE-9709-11 : AS and A Level - Problems and Solutions"