May-Jun-21-p1-CIE-0606/12 : Solution
2021 (May-June) CIE (0606-Additional Mathematics), Paper 1/12 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။
Write $\dfrac{(p q r)^{-2} r^{\frac{1}{3}}}{\left(p^{2} r\right)^{-1} q^{3}}$
in the form $p^{a} q^{b} r^{c}$, where $a, b$ and $c$ are constants.
[3]
SOLUTION
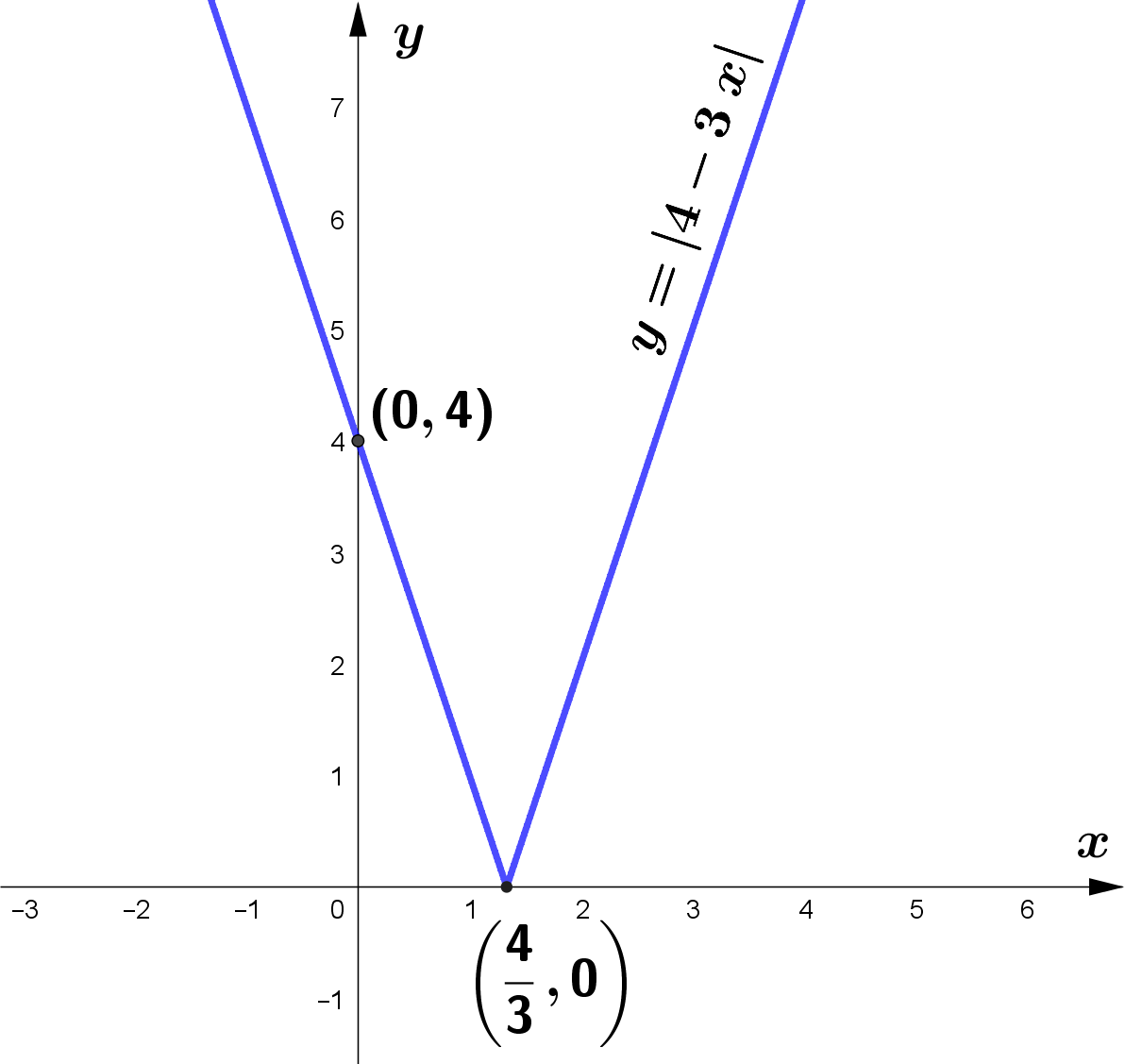
(a) On the axes, sketch the graph of $y=|4-3 x|$, stating the
intercepts with the coordinate axes.
[2]
(b) Solve the inequality $|4-3 x|\ge 7$.
[3]
SOLUTION
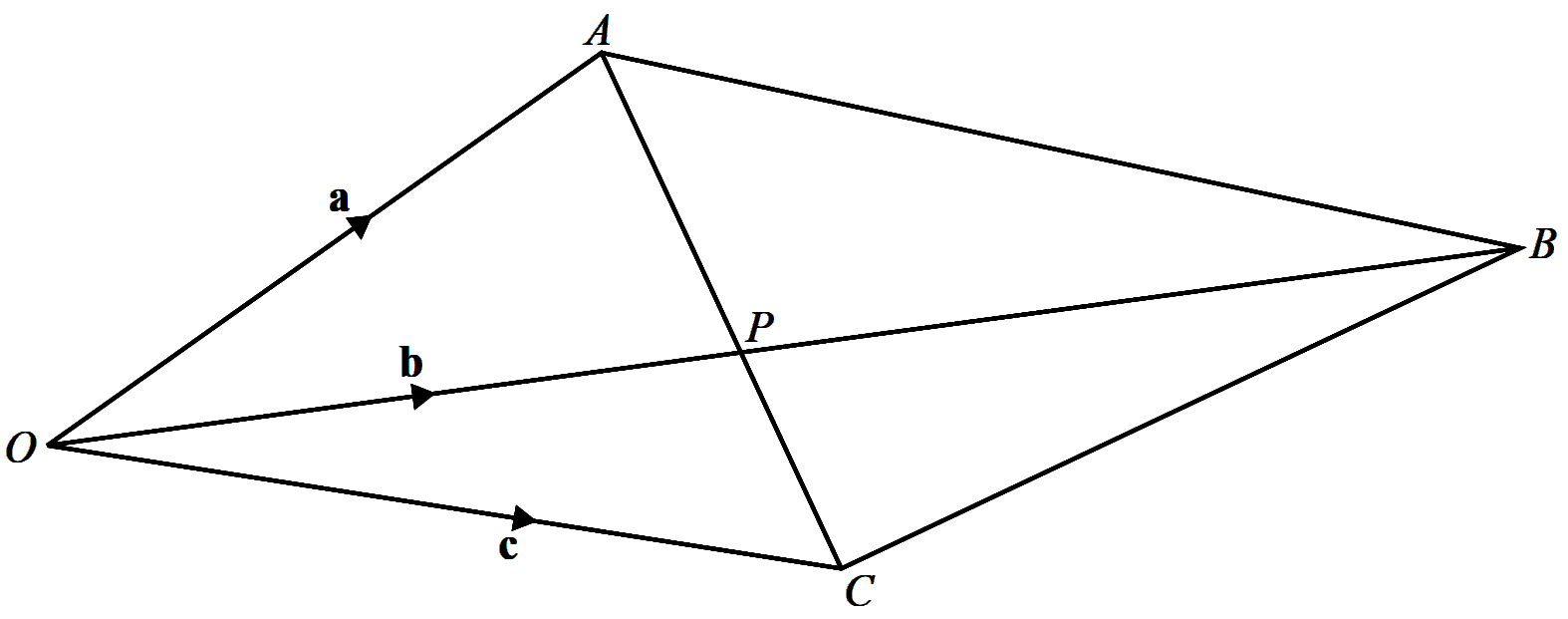
The diagram shows the quadrilateral $O A B C$ such that
$\overrightarrow{O A}=\mathbf{a}, \overrightarrow{O B}=\mathbf{b}$
and $\overrightarrow{O C}=\mathbf{c}$. The lines $O B$ and $A C$ intersect
at the point $P$, such that $A P: P C=3: 2$.
(a) Find $\overrightarrow{O P}$ in terms of $\mathbf{a}$ and $\mathbf{c}$.
[3]
(b) Given also that $O P: P B=2: 3$, show that
$2 \mathbf{b}=3 \mathbf{c}+2 \mathbf{a}$.
[2]
A curve is such that $\dfrac{d^{2} y}{d x^{2}}=(3 x+2)^{-\frac{1}{3}}$.
The curve has gradient $4$ at the point $(2,6.2)$.
Find the equation of the curve.
[6]
SOLUTION
(a) Given that $\log _{a} p+\log _{a} 5-\log _{a} 4=\log _{a} 20$,
find the value of $p$.
[2]
(b) Solve the equation $3^{2 x+1}+8\left(3^{x}\right)-3=0$.
[3]
(c) Solve the equation $4 \log _{y} 2+\log _{2} y=4$.
[3]
DO NOT USE A CALCULATOR IN THIS QUESTION.
A curve has equation $y=(3+\sqrt{5}) x^{2}-8 \sqrt{5} x+60$.
(a) Find the $x$-coordinate of the stationary point on the curve, giving your
answer in the form $a+b \sqrt{5}$, where $a$ and $b$ are integers.
[4]
(b) Hence find the $y$-coordinate of this stationary point, giving your answer
in the form $c \sqrt{5}$, where $c$ is an integer.
[3]
(a) A six-character password is to be made from the following eight characters.
$\begin{array}{llllll}\text { Digits } & \quad 1\quad & \quad 3\quad & \quad 5\quad & \quad 8\quad & \quad 9\quad \\\\
\text { Symbols } & \quad * \quad & \quad \$ \quad & \quad \# \quad & & \end{array}$
No character may be used more than once in a password.
Find the number of different passwords that can be chosen if
(i) there are no restrictions,
[1]
(ii) the password starts with a digit and finishes with a digit,
[2]
(iii) the password starts with three symbols.
[2]
(b) The number of combinations of 5 objects selected from $n$ objects is
six times the number of combinations of 4 objects selected from $n-1$ objects.
Find the value of $n$.
[3]
Variables $x$ and $y$ are such that $y=A x^{b}$, where $A$ and $b$ are constants.
When $\lg y$ is plotted against $\lg x$, a straight line graph passing through
the points $(0.61,0.57)$ and $(5.36,4.37)$ is obtained.
(a) Find the value of $A$ and of $b$.
[5]
Using your values of $A$ and $b$, find
(b) the value of $y$ when $x=3$,
[2]
(c) the value of $x$ when $y=3$.
[2]
SOLUTION
(a) The first three terms of an arithmetic progression are $-4,8,20$.
Find the smallest number of terms for which the sum of this arithmetic
progression is greater than 2000.
[4]
(b) The $7^{\text{ th}}$ and $9^{\text{ th}}$ terms of a geometric progression
are $27$ and $243$ respectively. Given that the geometric progression has a positive
common ratio, find
(i) this common ratio,
[2]
(ii) the $30^{\text{ th}}$ term, giving your answer as a power of $3 .$
[2]
(c) Explain why the geometric progression $1, \sin \theta, \sin ^{2} \theta, \ldots$
for $-\dfrac{\pi}{2}<\theta<\dfrac{\pi}{2}$,
where $\theta$ is in radians, has a sum to infinity.
[2]
(a) Solve the equation $\sin \alpha \operatorname{cosec}^{2} \alpha+\cos \alpha \sec ^{2} \alpha=0$ for $-\pi<\alpha<\pi$,
where $\alpha$ is in radians.
[4]
(b) (i) Show that $\dfrac{\cos \theta}{1-\sin \theta}+\dfrac{1-\sin \theta}{\cos \theta}=2 \sec \theta$.
[4]
(ii) Hence solve the equation $\dfrac{\cos 3 \phi}{1-\sin 3 \phi}+\dfrac{1-\sin 3 \phi}{\cos 3 \phi}=4$
for $0^{\circ} \leq \phi \leq 180^{\circ}$.
[4]
The normal to the curve $y=\dfrac{\ln \left(x^{2}+2\right)}{2 x-3}$ at the point
where $x=2$ meets the $y$-axis at the point $P$. Find the coordinates of $P$.
[7]
SOLUTION
$\begin{aligned}
& \dfrac{(p q r)^{-2} r^{\frac{1}{3}}}{\left(p^{2} r\right)^{-1} q^{3}} \\\\
=& \dfrac{p^{-2} q^{-2} r^{-2} r^{\frac{1}{3}}}{p^{-2} r^{-1} q^{3}} \\\\
=& p^{-2+2} q^{-2-3} r^{\frac{1}{3}+1} \\\\
=& p^{0} q^{-5} r^{\frac{4}{3}}
\end{aligned}$
$\begin{aligned}
y&=|4-3 x|\\\\
&=\left|-3\left(x-\frac{4}{3}\right)\right| \\\\
&=|-3|\left|\left(x-\frac{4}{3}\right)\right| \\\\
&=3\left|x-\frac{4}{3}\right|\\\\
\end{aligned}$
$\therefore$ The vertex point is $\left(\dfrac{4}{3}, 0\right)\\\\\\\\ $
When $x=0, y=3\left|0-\dfrac{4}{3}\right|=4\\\\\\\\ $.
$\therefore$ The $y$-intercept is $(0,4).$
$\begin{aligned}
|4-3 x| & \geq 7 \\\\
3\left|x-\frac{4}{3}\right| & \geq 7 \\\\
\left|x-\frac{4}{3}\right| & \geq \frac{7}{3} \\\\
x-\frac{4}{3} & \leq-\frac{7}{3} \text { or } x-\frac{4}{3} \geq \frac{7}{3} \\\\
x & \leq-1 \text { or } x \geq \frac{11}{3}
\end{aligned}$
SOLUTIONbr /> $\begin{aligned}
A P: P C &=3: 2 \\\\
\overrightarrow{O P} &=\frac{1}{5}(2 \overrightarrow{O A}+3 \overrightarrow{O C}) \\\\
&=\frac{1}{5}(2 \vec{a}+3 \vec{c})\\\\
\end{aligned}$
$O P: P B=2: 3$ and $O, P, B$ are collinear.
$\begin{aligned}
&\\
\therefore 3 \overrightarrow{O P} &=2 \overrightarrow{P B} \\\\
\therefore \overrightarrow{P B} &=\frac{3}{2} \overrightarrow{O P} \\\\
&=\frac{3}{10}(2 \vec{a}+3 \vec{c}) \\\\
\overrightarrow{O B} &=\overrightarrow{O P}+\overrightarrow{P B} \\\\
\vec{b} &=\frac{1}{5}(2 \vec{a}+3 \vec{c})+\frac{3}{10}(2 \vec{a}+3 \vec{c}) \\\\
&=\frac{1}{2}(2 \vec{a}+3 \vec{c}) \\\\
\therefore 2\vec{b} &=2 \vec{a}+3 \vec{c}
\end{aligned}$
$\begin{aligned}
\frac{d^{2} y}{d x^{2}} &=(3 x+2)^{-\frac{1}{3}} \\\\
\therefore\ \frac{d y}{d x} &=\displaystyle\int(3 x+2)^{-\frac{1}{3}} d x \\\\
\text { Let } u &=3 x+2 \\\\
d u &=3 d x \\\\
d x &=\frac{1}{3} d u\\\\
\therefore\ & \quad \displaystyle\int(3 x+2)^{-\frac{1}{3}} d x \\\\
&=\frac{1}{3} \displaystyle\int u^{-\frac{1}{3}} d u \\\\
&=\frac{1 / 3}{2 / 3} u^{2 / 3}+9 \\\\
&=\frac{1}{2} u^{2 / 3}+c_{1} \\\\
\therefore\ \frac{d y}{d x} &=\frac{1}{2}(3 x+2)^{\frac{2}{3}}+c_{1}\\\\
\left.\frac{d y}{d x}\right|_{(2,6.2)} &=4 \\\\
\frac{1}{2}(6+2)^{\frac{2}{3}}+c_{1} &=4 \\\\
2+c_{1} &=4 \\\\
\therefore\ c_{1} &=2 \\\\
\therefore\ \frac{d y}{d x} &=\frac{1}{2}(3 x+2)^{\frac{2}{3}}+2\\\\
y &=\displaystyle\int\left[\frac{1}{2}(3 x+2)^{\frac{2}{3}}+2\right] d x \\\\
&=\frac{1}{2} \displaystyle\int(3 x+2)^{\frac{2}{3}} d x+2 \int d x \\\\
&=\frac{1}{2} \times \frac{1}{3} \displaystyle\int(3 x+2)^{\frac{2}{3}} d(3 x+2)+2 \int d x \\\\
&=\frac{1}{10}(3 x+2)^{\frac{5}{3}}+2 x+c_{2}\\\\
\text{ When } x&=2, y=6.2\\\\
&6 \cdot 2=\frac{1}{10}(6+2)^{\frac{5}{3}}+4+c_{2} \\\\
&6 \cdot 2=3 \cdot 2+4+c_{2}\\\\
&\therefore\ c_{2}=-1 \\\\
&\therefore\ y=\frac{1}{10}(3 x+2)^{\frac{5}{3}}+2 x-1
\end{aligned}$
SOLUTION
$\begin{aligned}
\text { (a) }\quad \log _{a} p+\log _{a} 5-\log _{a} 4 &=\log _{a} 20 \\\\
\log _{a}\left(\frac{5 p}{4}\right) &=\log _{a} 20 \\\\
\therefore \quad \frac{5 p}{4} &=20 \\\\
5 p &=80 \\\\
p &=16\\\\
\text { (b) }\quad \qquad 3^{2 x+1}+8\left(3^{x}\right)-3&=0\\\\
3^{2 x} \cdot 3+8\left(3^{x}\right)-3&=0 \\\\
3\left(3^{x}\right)^{2}+8\left(3^{x}\right)-3&=0 \\\\
\left(3 \cdot 3^{x}-1\right)\left(3^{x}+3\right)&=0 \\\\
3^{x}=\frac{1}{3} \text { or } 3^{x}&=-3\\\\
\end{aligned}$
$\qquad$ Since $3^{x}>0$ for all $x \in \mathbb{R}$, $3^{x}=-3$ has no solution.
$\begin{aligned}
&\\
\qquad 3^{x}&=\frac{1}{3} \\\\
3^{x}&=3^{-1} \\\\
x&=-1\\\\
\end{aligned}$
$\begin{aligned}
\text { (c) } \qquad 4 \log _{y} 2+\log _{2} y &=4 \\\\
\frac{4}{\log _{2} y}+\log _{2} y &=4 \\\\
4+\left(\log _{2} y\right)^{2} &=4 \cdot \log _{2} y \\\\
\left(\log _{2} y\right)^{2}-4 \log y+4 &=0 \\\\
\left(\log _{2} y-2\right)^{2} &=0 \\\\
\log _{2} y &=2 \\\\
y &=4
\end{aligned}$
SOLUTION
$\begin{aligned}
&y =(3+\sqrt{5}) x^{2}-8 \sqrt{5} x+60 . \\\\
&\frac{d y}{d x} =2(3+\sqrt{5}) x-8 \sqrt{5}\\\\
\end{aligned}$
At stationary point,
$\begin{aligned}
&\\
\frac{d y}{d x} &=0 \\\\
2(3+\sqrt{5}) x-8 \sqrt{5} &=0 \\\\
x &=\frac{8 \sqrt{5}}{2(3+\sqrt{5})}\\\\
&=\frac{4 \sqrt{5}}{3+\sqrt{5}} \\\\
&=\frac{4 \sqrt{5}}{3+\sqrt{5}} \times \frac{3-\sqrt{5}}{3-\sqrt{5}} \\\\
&=\frac{12 \sqrt{5}=20}{9-5} \\\\
&=\frac{12 \sqrt{5}-20}{4} \\\\
&=-5+3 \sqrt{5}\\\\
\end{aligned}$
When $x=-5+3 \sqrt{5}$,
$\begin{aligned}
&\\
y &=(3+\sqrt{5})(-5+3 \sqrt{5})^{2}-8 \sqrt{5}(-5+3 \sqrt{5})+60 \\\\
&=(3+\sqrt{5})(25-30 \sqrt{5}+45)+40 \sqrt{5}-120+60 \\\\
&=(3+\sqrt{5})(70-30 \sqrt{5})+40 \sqrt{5}-60 \\\\
&=210-90 \sqrt{5}+70 \sqrt{5}-150+40 \sqrt{5}-60 \\\\
&=20 \sqrt{5}\\\\
\end{aligned}$
$\text{ (a) }$ (i) number of ways to form different passwords $={}^8P_{6}=20160$ ways.
$\quad\ $ (ii) number of ways to form different passwords starting with a digit and ending with a digit.
$={}^5P_{2} \times{ }^{6}P_{4}=7200$ ways.
$\quad\ $ (iii) number of ways to form different passwords starting with three symbols
$=3 ! \times {}^5P_{3}=360 $ ways.
$\begin{aligned}
&\\
\text{ (b) } \hspace{2cm} { }^{n} C_{5} &=6 \times{ }^{n-1} C_{4} \\\\
\frac{n !}{5 !(n-5) !} &=6 \times \frac{(n-1) !}{4 !(n-1-4) !} \\\\
\frac{n(n-1) !}{5 \times 4 !(n-5) !} &=\frac{6 \times(n-1) !}{4 !(n-5) !} \\\\
\frac{n}{5} &=6 \\\\
n &=30
\end{aligned}$
$\begin{aligned}
\text{ (a) }\quad y &=A x^{b} \\\\
\lg y &=\lg \left(A x^{b}\right) \\\\
\lg y &=\lg A+b \lg x \\\\
0.57 &=\lg A+0.616 \ldots(1) \\\\
5.36 &=\lg A+4.37 b \ldots(2)\\\\
\end{aligned}$
$\quad$ Solving equations $(1)$ and $(2)$
$\begin{aligned}
&\\
b &=0.8 \\\\
\lg A &=0.082 \\\\
A &=10^{0.082} \\\\
&=1.21\\\\
\therefore\ y&=1.21\left(x^{0.8}\right)\\\\
\text{ (b) }\quad \text{ When } x&=3\\\\
y &=1.21(3)^{0.8} \\\\
&=2.91 \\\\
\text{ (c) }\quad \text { When } y &=3, \\\\
3 &=1.21\left(x^{0.8}\right) \\\\
x^{0.8} &=\frac{3}{1.21} \\\\
x &=\left(\frac{3}{1.21}\right)^{1.25} \\\\
&=3.11
\end{aligned}$
SOLUTION
$\text{ (a) } \quad -4,8,20, \ldots$ is an A.P.
$\begin{aligned}
&\\
\therefore\ a &=-4 \\\\
d &=8-(-4) \\\\
&=12 \\\\
S_{n} &>2000 \\\\
\frac{n}{2}\{2 a+(n-1) d\} &>2000 \\\\
\frac{n}{2}\{-8+(n-1) 12\} &>2000 \\\\
n\{-2+3 n-3\} &>1000\\\\
3 n^{2}-5 n &>1000 \\\\
n^{2}-\frac{5}{3} n &>\frac{1000}{3} \\\\
n-\frac{5}{3} n+\left(\frac{5}{6}\right)^{2} &>\frac{1000}{3}+\left(\frac{5}{6}\right)^{2} \\\\
\left(n-\frac{5}{6}\right)^{2} &>334.03 \\\\
n-\frac{5}{6} &>18.28 \\\\
n &>19.1 \\\\
\therefore n &=20\\\\
\end{aligned}$
$\therefore$ The smalles number of terms $=20\\\\ $
$\text{ (b) }$ In a G.P,
$\begin{aligned}
&\\
\text{ (i) } \quad u_{7} &=27 \\\\
a r^{6} &=27 \cdots(1) \\\\
u_{9} &=243 \\\\
a r^{8} &=243 \cdots(2) \\\\
\frac{a r^{8}}{a r^{6}}&= \frac{243}{27} \\\\
r^{2} &=9 \\\\
\therefore\ r &=3\\\\
\therefore\ a\left(3^{6}\right) &=27 \\\\
a &=\frac{3^{3}}{3^{6}} \\\\
&=\frac{1}{3^{3}} \\\\
u_{30} &=a r^{29} \\\\
&=\frac{1}{3^{3}} \times 3^{29} \\\\
&=3^{26}\\\\
\end{aligned}$
$\text{ (c) } \quad 1, \sin \theta, \sin ^{2} \theta, \ldots$ is a GP, where
$\begin{aligned}
&\\
&r =\frac{\sin \theta}{1} \\\\
&\ \ =\sin \theta \\\\
&\text { Since }-\frac{\pi}{2}<\theta <\frac{\pi}{2}\\\\
&\sin \left(-\frac{\pi}{2}\right)<\sin \theta <\sin \frac{\pi}{2} \\\\
&-1< r <1 \\\\
&\therefore\ |r| <1\\\\
\end{aligned}$
Hence, the series is convergent and sum to infinity exists.
SOLUTION
$\begin{aligned}
\text{ (a) }\quad\sin \alpha \operatorname{cosec}^{2} \alpha+\cos \alpha \sec ^{2} \alpha & =0,-\pi<\alpha<\pi\\\\
\frac{1}{\sin \alpha}+\frac{1}{\cos \alpha} &=0 \\\\
\frac{1}{\cos \alpha} &=-\frac{1}{\sin \alpha} \\\\
\therefore \frac{\sin \alpha}{\cos \alpha} &=-1 \\\\
\tan \alpha &=-1 \\\\
\alpha=-\frac{\pi}{4} \quad \text { or } \alpha &=\frac{3 \pi}{4}\\\\
\end{aligned}$
$\begin{aligned}
\text{ (b) (i) }\quad & \frac{\cos \theta}{1-\sin \theta}+\frac{1-\sin \theta}{\cos \theta} \\\\
=&\ \frac{\cos ^{2} \theta+1-2 \sin \theta+\sin ^{2} \theta}{(1-\sin \theta) \cos \theta} \\\\
=&\ \frac{2-2 \sin \theta}{(1-\sin \theta) \cos \theta} \\\\
=&\ \frac{2(1-\sin \theta)}{(1-\sin \theta) \cos \theta} \\\\
=&\ \frac{2}{\cos \theta}=2 \sec \theta\\\\
\end{aligned}$
$\text{ (ii) }\quad\dfrac{\cos 3 \phi}{1-\sin 3 \phi}+\dfrac{1-\sin 3 \phi}{\cos 3 \phi}=4\\\\ $
$\qquad$ By part (i),
$\begin{aligned}
&\\
\frac{2}{\cos 3 \phi} &=4 \\\\
\cos 3 \phi &=\frac{1}{2} \\\\
3 \phi=60^{\circ} \text { or } 3 \phi &=300^{\circ} \text { or } 3 \phi=420^{\circ} \\\\
\phi=20^{\circ} \text { or } \phi &=100^{\circ} \text { or } \phi=140^{\circ}
\end{aligned}$
$\begin{aligned}
\text{Curve }: y&=\dfrac{\ln \left(x^{2}+2\right)}{2 x-3}\\\\
\dfrac{d y}{d x} &=\dfrac{(2 x-3) \dfrac{d}{d x} \ln \left(x^{2}+2\right)-\ln \left(x^{2}+2\right) \dfrac{d}{d x}(2 x-3)}{(2 x-3)^{2}} \\\\
&=\dfrac{(2 x-3) \dfrac{2 x}{x^{2}+2}-2 \ln \left(x^{2}+2\right)}{(2 x-3)^{2}} \\\\
&=\dfrac{2}{(2 x-3)^{2}}\left[\dfrac{x(2 x-3)}{x^{2}+2}-\ln \left(x^{2}+2\right)\right]\\\\
\end{aligned}$
$\begin{aligned}
\left.\dfrac{d y}{d x}\right|_{x=2} &=\dfrac{2}{(4-3)^{2}}\left[\dfrac{2(4-3)}{4+2}-\ln (4+2)\right] \\\\
&=2\left[\dfrac{1}{3}-\ln 6\right] \\\\
&=\dfrac{2(1-3 \ln 6)}{3} \\\\
\therefore \text { Gradient of normal } &=-\dfrac{3}{2(1-3 \ln 6)} \\\\
&=\dfrac{3}{2(3 \ln 6-1)}\\\\
\text{ When } x&=2,\\\\
y&=\ln 6\\\\
\end{aligned}$
$\therefore$ The equation of normal at $(2, \ln 6)$ is
$\begin{aligned}
&\\
y-\ln 6 &=\dfrac{3}{2(3 \ln 6-1)}(x-2) \\\\
y &=\dfrac{3}{2(3 \ln 6-1)}(x-2)+\ln 6\\\\
\text{ When } x&=0,\\\\
y &=\dfrac{3}{1-3 \ln 6}+\ln 6 \\\\
&=1.11\\\\
\end{aligned}$
$\therefore$ The coordinates of the point $P$ is $(0,1.11).$

Post a Comment for "May-Jun-21-p1-CIE-0606/12 : Solution"