May-Jun-21-p1-CIE-0606/11 : Solution
2021 (May-June) CIE (0606-Additional Mathematics), Paper 1 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။
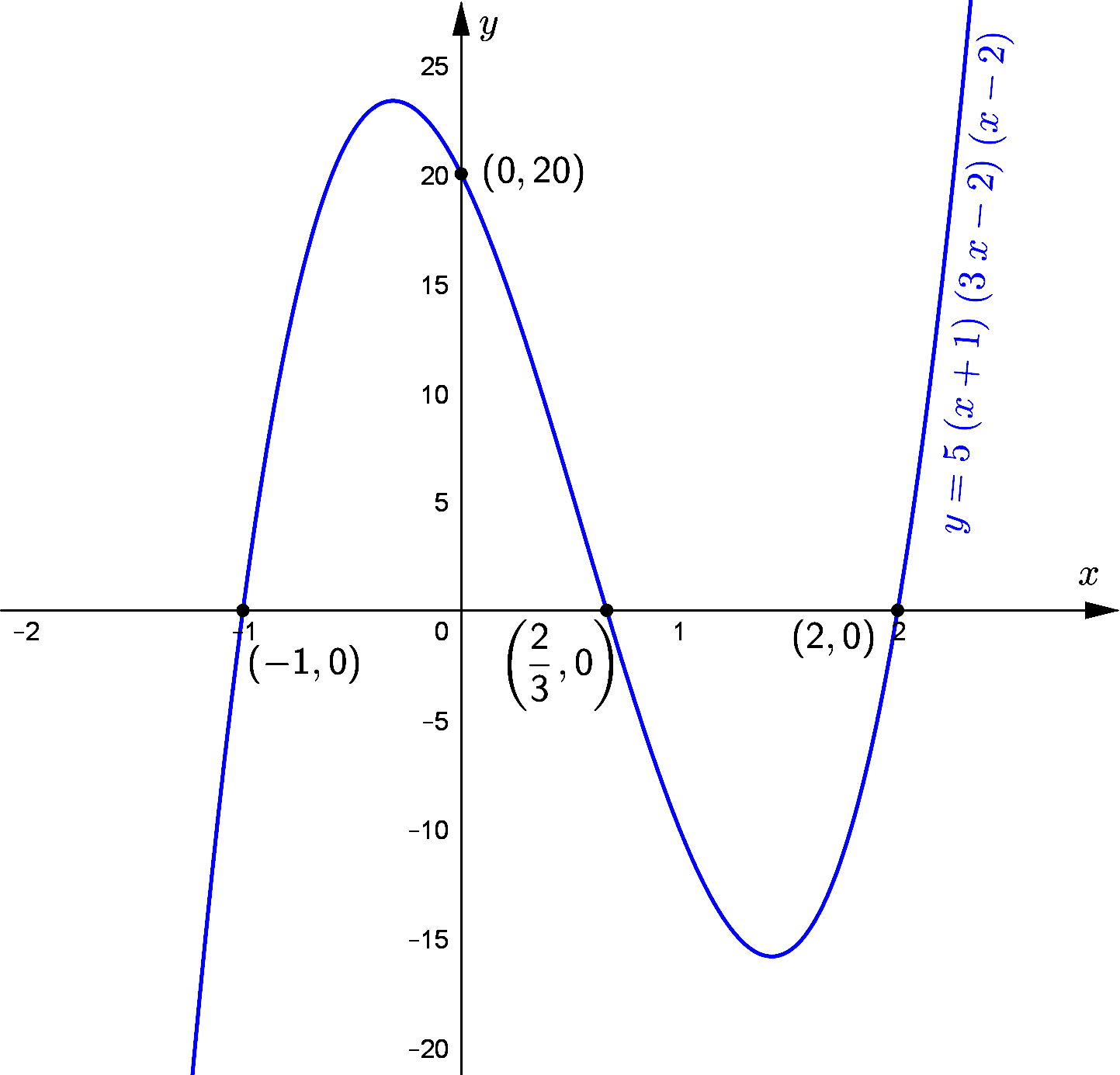
(a) On the axes, sketch the graph of $y = 5(x+1)(3x-2)(x-2)$, stating the intercepts
with the coordinate axes.
[3]
(b) Hence find the values of x for which $5(x+1)(3x-2)(x-2)>0$ .
[2]
SOLUTION
Find $\displaystyle\int_{3}^{5}\left(\dfrac{1}{x-1}-\dfrac{1}{(x-1)^{2}}\right) \mathrm{d} x$,
giving your answer in the form $a+\ln b$, where $a$ and $b$ are rational numbers.
[5]
The polynomial $p(x)=a x^{3}-9 x^{2}+b x-6$, where $a$ and $b$ are constants,
has a factor of $x-2 .$ The polynomial has a remainder of $66$ when divided by $x-3$.
(a) Find the value of $a$ and of $b$.
[4]
(b) Using your values of $a$ and $b$, show that $p(x)=(x-2)q(x)$ , where $q(x)$ is
a quadratic factor to be found.
[2]
(c) Hence show that the equation $p(x) = 0$ has only one real solution.
[2]
SOLUTION
The first 3 terms in the expansion of $(a+x)^{3}\left(1-\dfrac{x}{3}\right)^{5}$,
in ascending powers of $x$, can be written in the form $27+b x+c x^{2}$, where $a, b$
and $c$ are integers. Find the values of $a, b$ and $c$.
[8]
SOLUTION
The functions $f$ and $g$ are defined as follows.
$\begin{aligned}
&\\
&f(x)=x^{2}+4 x \text { for } x \in \mathbb{R} \\\\
& g(x)=1+e^{2 x} \text { for } x \in \mathbb{R}\\\\
\end{aligned}$
(a) Find the range of $f$.
[2]
(b) Write down the range of $g$.
[1]
(c) Find the exact solution of the equation $fg(x) = 21$,
giving your answer as a single logarithm.
[4]
SOLUTION
(a) (i) Find how many different 5-digit numbers can be formed using the digits
1, 3, 5, 6, 8 and 9. No digit may be used more than once in any 5-digit number.
[1]
(ii) How many of these 5-digit numbers are odd?
[1]
(iii) How many of these 5-digit numbers are odd and greater than 60000?
[3]
(b) Given that $45 \times{ }^{n} \mathrm{C}_{4}=(n+1) \times{ }^{n+1} \mathrm{C}_{5}$,
find the value of $n$.
[4]
SOLUTION
(a) In this question, all lengths are in metres and time, t, is in seconds.
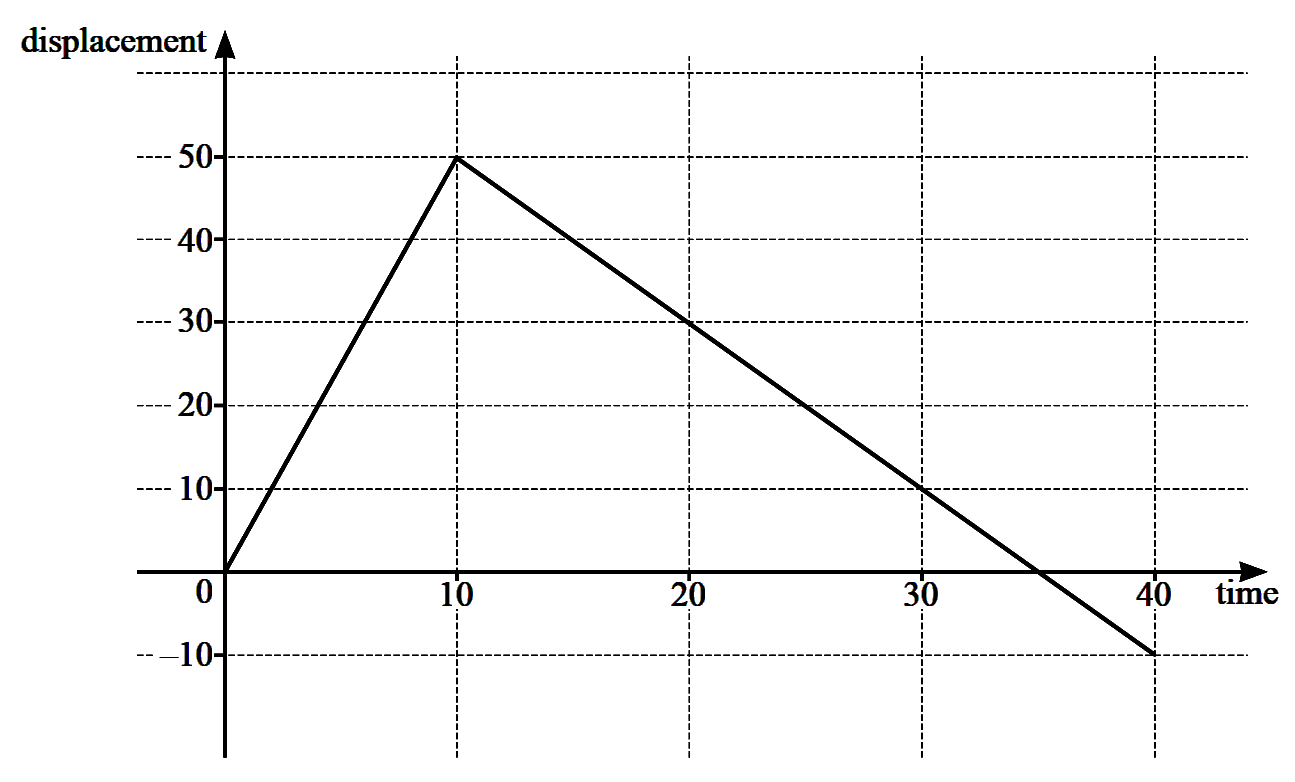
The diagram shows the displacement–time graph for a runner, for $0\le t\le 40$.
(i) Find the distance the runner has travelled when $t = 40$.
[1]
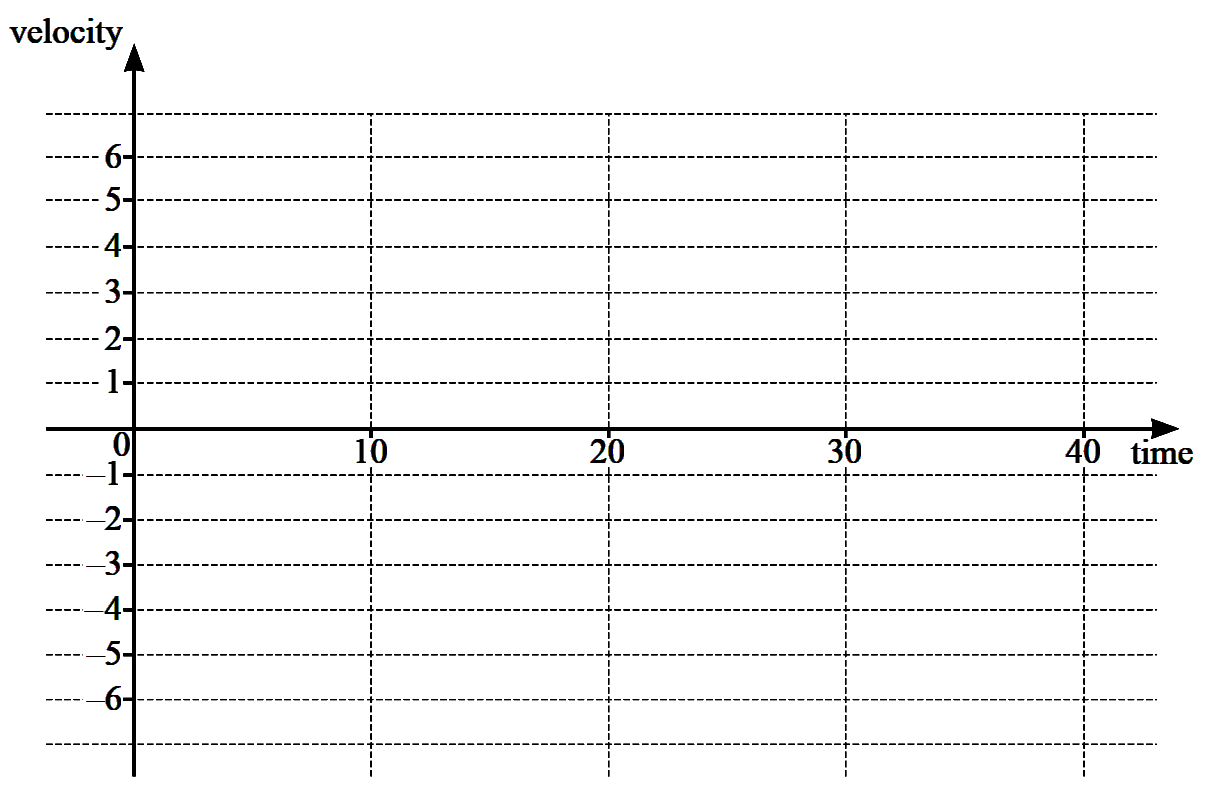
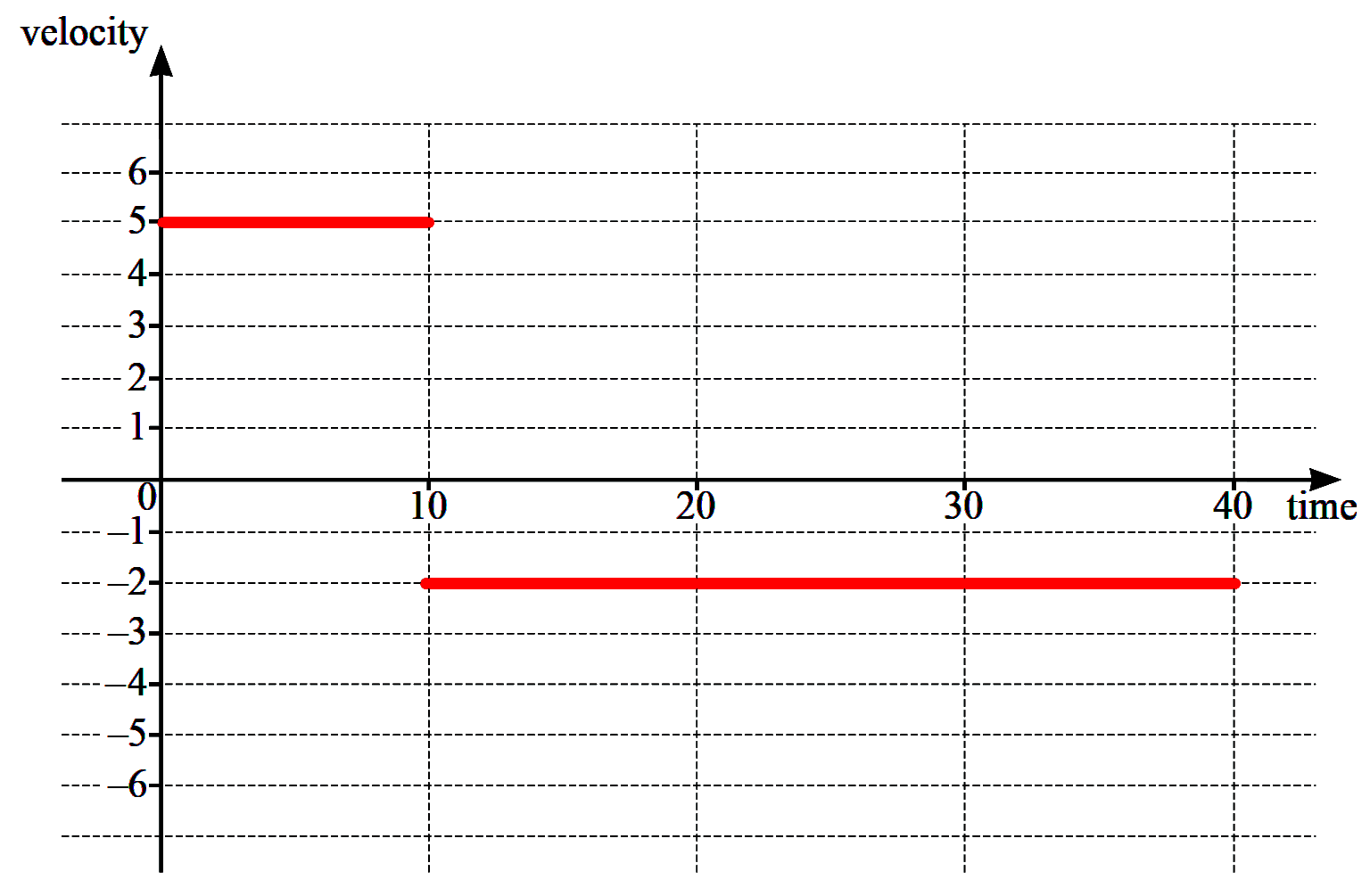
(ii) On the axes, draw the corresponding velocity–time graph for the runner, for $0\le t\le 40$.
[2]
(b) A particle, $P$, moves in a straight line such that its displacement from
a fixed point at time $t$ is $s$. The acceleration of $P$ is given by
$(2 t+4)^{-\frac{1}{2}}$, for $t>0$.
(i) Given that $P$ has a velocity of $9$ when $t=6$, find the velocity of $P$ at time $t$.
[3]
(ii) Given that $s=\dfrac{1}{3}$ when $t=6$, find the displacement of $P$ at time $t$.
[3]
SOLUTION
DO NOT USE A CALCULATOR IN THIS QUESTION.
A curve has equation $y=(2-\sqrt{3}) x^{2}+x-1$. The $x$-coordinate of a point $A$
on the curve is $\dfrac{\sqrt{3}+1}{2-\sqrt{3}}$.
(a) Show that the coordinates of $A$ can be written in the form $(p+q \sqrt{3}, r+s \sqrt{3})$,
where $p, q, r$ and $s$ are integers.
[5]
(b) Find the $x$-coordinate of the stationary point on the curve, giving your answer
in the form $a+b \sqrt{3}$, where $a$ and $b$ are rational numbers.
[3]
SOLUTION
(a) (i) Write $6 x y+3 y+4 x+2$ in the form $(a x+b)(c y+d)$, where $a, b, c$ and $d$
are positive integers.
[1]
(ii) Hence solve the equation $6 \sin \theta \cos \theta+3 \cos \theta+4 \sin \theta+2=0$
for $0^{\circ} <\theta<360^{\circ}$.
[4]
(b) Solve the equation $\dfrac{1}{2} \sec \left(2 \phi+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{3}}$
for $-\pi<\phi<\pi$, where $\phi$ is in radians. Give your answers in terms of $\pi$.
[5]
SOLUTION
In this question all lengths are in centimetres.
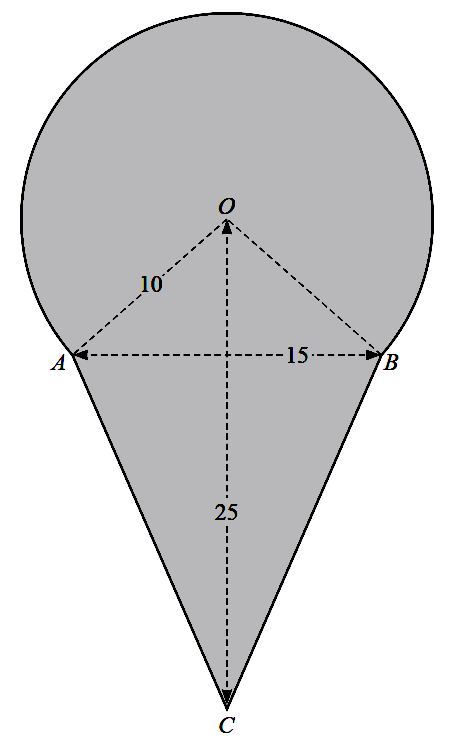
The diagram shows a shaded shape. The arc $AB$ is the major arc of a circle, centre $O$, radius $10$.
The line $AB$ is of length $15$, the line $OC$ is of length $25$ and the lengths of $AC$ and $BC$ are
equal.
(a) Show that the angle $AOB$ is $1.70$ radians correct to $2$ decimal places.
[2]
(b) Find the perimeter of the shaded shape.
[4]
(c) Find the area of the shaded shape.
[5]
SOLUTION
(a) $y=5(x+1)(3 x-2)(x-2)\\\\ $
When $y=0$,
$\begin{aligned}
&\\
&5(x+1)(3 x-2)(x-2)=0 \\\\
&\therefore\ x=-1 \text { or } x=\dfrac{2}{3} \text { or } x=2\\\\
\end{aligned}$
$\therefore$ The graph cuts $x$-axis at $(-1,0),\left(\dfrac{2}{3}, 0\right)$ and $(2,0)$.
When $x=0, y=20\\\\ $.
The graph cuts $y$ axis at $(0,20)$.
(b) The set of the values of $x$ to satisfy the inequality $5(x+1)(3 x-2)(x-2)>0$ is
$\left\{x \mid-1<x<\dfrac{2}{3} \text { or } x>2\right\}. $
SOLUTION
$\begin{aligned}
\text { let } u&=x-1 \\\\
\therefore\ d u&=d x \\\\
\text { When } x&=3, u=2 \\\\
\text { When } x&=5, u=4\\\\
\end{aligned}$
$\begin{aligned}
& \int_{3}^{5}\left(\frac{1}{x-1}-\frac{1}{(x-1)^{2}}\right) d x \\\\
=& \int_{2}^{4}\left(\frac{1}{u}-\frac{1}{u^{2}}\right) d u \\\\
=& \int_{2}^{4} \frac{1}{u} d u-\int_{2}^{4} \frac{1}{u^{2}} d u \\\\
=& \int_{2}^{4} \frac{1}{u} d u-\int_{2}^{4} u^{-2} d u \\\\
=&\left.\ln u\right]_{2}^{4}+\left.\frac{1}{u}\right]_{2}^{4} \\\\
=&(\ln 4-\ln 2)+\frac{1}{4}-\frac{1}{2} \\\\
=& \ln \frac{4}{2}-\frac{1}{4} \\\\
=&-\frac{1}{4}+\ln 2
\end{aligned}$
$\begin{aligned}
\text{(a) } \quad &p(x)=a x^{3}-9 x^{2}+b x-6 \\\\
& x-2 \text { is a factor of } p(x) . \\\\
\therefore\ & p(2)=0 \\\\
& 8 a-3 b+2 b-6=0 \\\\
& 4 a+b=21 \ldots(1)\\\\
\end{aligned}$
$\quad $ When $p(x)$ is divided by $(x-3)$,
$\begin{aligned}
&\\
\quad\ \text{ the remainder } &=p(3)\\\\
\therefore\ p(3)&=66\\\\
27 a-81+3 b-6 &=66 \\\\
9 a+b &=51 \ldots(2)\\\\
\end{aligned}$
Solving equation $(1)$ and $(2)$,
$\begin{aligned}
&\\
\quad &a=6 \text { and } b=-3 \\\\
&\therefore p(x)=6 x^{3}-9 x^{2}-3 x-6\\\\
\end{aligned}$
$\text{(b) } \quad\ $ Let $6 x^{3}-9 x^{2}-3 x-6=(x-2)\left(6 x^{2}+k x+3\right)$.
$\begin{aligned}
&\\
\quad\ \therefore\ 6 x^{3}-9 x^{2}-3 x-6 &=6 x^{3}-12 x^{2}+k x^{2}-2 k x+3 x-6 \\\\
&=6 x^{3}+(k-12) x^{2}+(3-2 k) x-6 \\\\
\therefore\ k-12 &=-9 \\\\
\therefore\ k &=3 \\\\
\therefore\ 6 x^{3}-9 x^{2}-8 x-6 &=(x-2)\left(6 x^{2}+3 x+3\right)\\\\
\therefore\ q(x) &=6 x^{2}+3 x+3 \\\\
\end{aligned}$
$\begin{aligned}
\text{(c) } \quad\ \text { When } 6 x^{3}-9 x^{2}-8 x-6 &=0 \\\\
(x-2)\left(6 x^{2}+3 x+3\right) &=0 \\\\
6(x-2)\left(x^{2}+\dfrac{1}{2} x+\dfrac{1}{2}\right) &=0 \\\\
(x-2)\left(x^{2}+\dfrac{1}{2} x+\dfrac{1}{16}+\dfrac{7}{16}\right) &=0 \\\\
(x-2)\left(\left(x+\dfrac{1}{4}\right)^{2}+\dfrac{7}{16}\right) &=0 \\\\
\text{Since } \left(x+\dfrac{1}{4}\right)^{2}+\dfrac{7}{16} &>0, \\\\
x-2 &=0 \\\\
\therefore\ x &=2\\\\
\end{aligned}$
$\therefore$ There is only one real solution for $p(x)=0$.
$\begin{aligned}
(a+x)^{3}\left(1-\frac{x}{3}\right)^{5} &=27+b x+c x^{2}+\cdots \\\\
\left(a^{3}+3 a^{2} x+3 a x^{2}+x^{3}\right)\left(1-5\left(\frac{x}{3}\right)+10\left(\frac{x}{3}\right)^{2}+\cdots\right) &=27+b x+c x^{2}+\cdots \\\\
\left(a^{3}+3 a^{2} x+3 a x^{2}+x^{3}\right)\left(1-\frac{5 x}{3}+\frac{10 x^{2}}{9}+\cdots\right) &=27+b x+c x^{2}+\cdots \\\\
\left(a^{3}-\frac{5 a^{3}}{3} x+\frac{10 a^{3}}{9} x^{2}+3 a^{2} x-5 a^{2} x^{2}+3 a x^{2}+\cdots\right) &=27+b x+c x^{2}+\cdots \\\\
a^{3}+\left(3 a^{2}-\frac{5 a^{3}}{3}\right) x+\left(\frac{10 a^{3}}{9}-5 a^{2}+3 a\right) x^{2}+\cdots &=27+b x+c x^{2}+\cdots\\\\
\end{aligned}$
$\begin{aligned}
\quad\therefore\quad a^{3} &=27 \\\\
a &=3\\\\
b &=3 a^{2}-\frac{5 a^{3}}{3} \\\\
&=3\left(3^{2}\right)-\frac{5(27)}{3} \\\\
&=27-45 \\\\
&=-18 \\\\
c &=\frac{10 a^{3}}{9}-5 a^{2}+3 a \\\\
&=\frac{10(27)}{9}-5(3)^{2}+3(3) \\\\
&=30-45+9 \\\\
&=-6
\end{aligned}$
$\begin{aligned}
\text{(a) } \hspace{1.5cm} f(x) &=x^{2}+4 x, x \in R \\\\
f(x) &=x^{2}+4 x+4-4 \\\\
f(x) &=(x+2)^{2}-4 \\\\
(x+2)^{2} & \geq 0 \text { for all } x \in \mathbb{R} \\\\
(x+2)^{2}-4 & \ge-4 \\\\
\therefore \quad f(x) & \ge-4\\\\
\text{(b) }\hspace{1.5cm} g(x)&=1+e^{2 x}, x \in \mathbb{R}\\\\
\end{aligned}$
$\qquad$ Since $e^{2 x}>0$ for all $x \in \mathbb{R}$,
$\begin{aligned}
&\\
1+e^{2 x} &>1 \\\\
\therefore\ g(x) &>1\\\\
\text{(c) }\hspace{2cm} f g(x)&=21\\\\
f(g(x)) &=21 \\\\
f\left(1+e^{2 x}\right) &=21 \\\\
\left(1+e^{2 x}+2\right)^{2}-4 &=21 \\\\
\left(e^{2 x}+3\right)^{2} &=25 \\\\
e^{2 x}+3 &=5 \\\\
e^{2 x} &=2 \\\\
2 x &=\ln 2 \\\\
x &=\frac{1}{2} \ln 2 \\\\
&=\ln \sqrt{2}
\end{aligned}$
$\begin{aligned}
\text{(a) (i) } \quad & { }^{6} P_{5}=720\\\\
\quad\text{(ii) }\quad & \text{Total number of 5-digit odd numbers} \\\\
=&\ 4 \times 5 ! \\\\
=&\ 480\\\\
\text{(iii) } \quad &\text{Total number of 5-digit odd numbers start with 6 and 8}\\\\
=&\ 2 \times 4 \times 3 \times 2 \\\\
=&\ 192\\\\
&\text{Total number of 5 -digit odd numbers start with 9 }\\\\
=&\ \times 4 \times 3 \times 3 \\\\
=&\ 72\\\\
\therefore\ &\text{Total number of 5-digit odd numbers } > 6000\\\\
=&\ 192+72 \\\\
=&\ 264\\\\
\end{aligned}$
$\begin{aligned}
\text{(c) } \hspace{1.5cm} 45 \times{ }^{n} C_{4} &=(n+1) \times{ }^{n+1} C_{5} \\\\
45 \times \frac{n !}{4 !(n-4) !}&=(n+1) \times \frac{(n+1) !}{5 !(n+1-5) !}\\\\
4 !(n-4) ! &=(n+1) \times \frac{(n+1) n !}{5 \times 4 !(n-4) !} \\\\
45 &=\frac{(n+1)^{2}}{5} \\\\
(n+1)^{2} &=225\\\\
n+1 &=15 \\\\
n &=14
\end{aligned}$
(i) At $0 \leq t <10$
distance travelled by runner $=50 \mathrm{~m}$
At $10 \leq t<40$,
distance travelled by runner $=60 \mathrm{~m}$
the distance the runner has travelled when $t=40$ is
$(50+60)=110 \mathrm{~m}$
(ii) $0 \leqslant t<10$,
$\quad v=\dfrac{50}{10}=5 \mathrm{~m} / \mathrm{s}$
$\quad 10 \leq t \leq 40$,
$\quad v=\dfrac{-10-50}{40-10}=\dfrac{-60}{30}=-2 \mathrm{~m} / \mathrm{s}$
$\begin{aligned}
\text { (b) } \quad \text { displacement } &=s\\\\
\text { velocity } &=\frac{d s}{d t} \\\\
\text { acceleration } &=\frac{d^{2} s}{d t^{2}} \\\\
\frac{d^{2} s}{d t} &=(2 t+4)^{-1 / 2}, t>0 \\\\
\text { velocity } &=\displaystyle\int(2 t+4)^{-1 / 2} d t\\\\
\text { Let } u &=2 t+4 \\\\
d u &=2 d t \\\\
d t &=\frac{1}{2} d u \\\\
\text { velocity } &=\frac{1}{2} \int u^{-1 / 2} d u \\\\
&=\sqrt{u}+c_{1} \\\\ &=\sqrt{2 t+4}+c_{1} \\\\
\text { When } t &=6, v=9 . \\\\
9 &=\sqrt{16}+c_{1} \\\\
c_{1} &=5 \\\\
\therefore\ \frac{d s}{d t} &=\sqrt{2 t+4}+5 \text { (at time t) } \\\\
\text { displacement } &=\int(\sqrt{2 t+4}+5) d t \\\\
&=\int \sqrt{2 t+4} d t+5 \int d t \\\\
&=\frac{1}{2}(2 t+4)^{3 / 2}+5 t+c_{2}\\\\
s &=\frac{1}{3} \text { When } t=6 \\\\
\frac{1}{3} &=\frac{1}{3}(12+4)^{3 / 2}+5(6)+c_{2} \\\\
\frac{1}{3} &=\frac{1}{3}(64)+30+c_{2} \\\\
\therefore\ c_{2} &=-51 \\\\
\therefore\ s &=\frac{1}{3}(2 t+4)^{3 / 2}+5 t-51
\end{aligned}$
$\begin{aligned}
\text{ (a) } \quad \text{ Curve } : y&=(2-\sqrt{3}) x^{2}+x-1\\\\
\frac{\sqrt{3}+1}{2-\sqrt{3}} &=\frac{\sqrt{3}+1}{2-\sqrt{3}} \times \frac{2+\sqrt{3}}{2+\sqrt{3}} \\\\
&=\frac{2 \sqrt{3}+3+2+\sqrt{3}}{4-3} \\\\
&=5+3 \sqrt{3}\\\\
\text{ When } x&=5+3 \sqrt{3},\\\\
y &=(2-\sqrt{3})(5+3 \sqrt{3})^{2}+5+3 \sqrt{3}-1 \\\\
&=(2-\sqrt{3})(25+30 \sqrt{3}+27)+4+3 \sqrt{3}\\\\
y &=(2-\sqrt{3})(52+30 \sqrt{3})+4+3 \sqrt{3} \\\\
y &=104-52 \sqrt{3}+60 \sqrt{3}-90+4+3 \sqrt{3} \\\\
&=18+11 \sqrt{3}\\\\
\end{aligned}$
$\qquad \therefore$ The coordinates of the point $A$ is
$(5+3 \sqrt{3}, 18+11 \sqrt{3}).$
$\begin{aligned}
&\\
\text{ (b) } \quad \frac{d y}{d x}&=2(2-\sqrt{3}) x+1
\end{aligned}\\\\ $
$\qquad$ At stationary point,
$\begin{aligned}
&\\
\frac{d y}{d x} &=0 . \\\\
\qquad 2(2-\sqrt{3}) x+1 &=0 \\\\
x &=\frac{1}{2 \sqrt{3}-4}\\\\
x &=\frac{1}{2 \sqrt{3}-4} \times \frac{2 \sqrt{3}+4}{2 \sqrt{3}+4} \\\\
&=\frac{2 \sqrt{3}+4}{12-16} \\\\
&=\frac{2 \sqrt{3}+4}{-4} \\\\
&=-1-\frac{\sqrt{3}}{2}\\\\
\end{aligned}$
$\begin{aligned}
\text { (a) (i) }\quad & 6 x y+3 y+4 x+2 \\\\
=& 3 y(2 x+1)+2(2 x+1) \\\\
=&(2 x+1)(3 y+2)\\\\
\end{aligned}$
$\begin{aligned}
\quad\text{ (ii) } \quad 6 \sin \theta \cos \theta+3 \cos \theta+4 \sin \theta+2&=0\\\\
\therefore(2 \sin \theta+1)(8 \cos \theta+2) &=0 \\\\
\sin \theta=-\frac{1}{2} \text { or } \cos \theta &=-\frac{2}{3}\\\\
\end{aligned}$
$\begin{aligned}
\qquad\text { For } \sin \theta &=-\frac{1}{2} \\\\
\theta &=210^{\circ} \text { or } \\\\
\theta &=330^{\circ} \\\\
\text { For } \cos \theta &=-\frac{2}{3} \\\\
\theta &=180-48.2 \text { or } \\\\
\theta &=180^{\circ}+48.2^{\circ} \\\\
\therefore \theta &=131.8^{\circ} \text { or } \\\\
\theta &=228.2^{\circ}\\\\
\end{aligned}$
$\begin{aligned}
\text { (a) (i) } &\quad \frac{1}{2} \sec \left(2 \phi+\frac{\pi}{4}\right)=\frac{1}{\sqrt{3}},-\pi<\phi<\pi \\\\
&\sec \left(2 \phi+\frac{\pi}{4}\right)=\frac{2}{\sqrt{3}} \\\\
&\cos \left(2 \phi+\frac{\pi}{4}\right)=\frac{\sqrt{3}}{2}\\\\
\end{aligned}$
$\qquad \therefore$ basic acute angle (reference angle) $=\dfrac{\pi}{6}$
$\begin{aligned}
&\\
\qquad \cos \left(2 \phi+\frac{\pi}{4}\right)&>0 \\\\
\end{aligned}$
$\qquad \therefore 2 \phi+\dfrac{\pi}{4}$ lies either
in the $1^{\text {st }}$ or $4^{\text {th }}$
quadrant.
$\begin{aligned}
&\\
\qquad 2 \phi+\frac{\pi}{4} &=\frac{\pi}{6} \text { or } \\\\
2 \phi+\frac{\pi}{4}&=-\frac{\pi}{6} \text { or }\\\\
2 \phi+\frac{\pi}{4}&=\frac{13 \pi}{6} \text { or }\\\\
2 \phi+\frac{\pi}{4}&=\frac{11 \pi}{6} \\\\
\qquad \therefore \phi &=-\frac{\pi}{24} \text { or }\\\\
\phi&=-\frac{5 \pi}{24} \text { or } \\\\
\phi&=\frac{23 \pi}{24} \text { or } \\\\
\phi&=\frac{19 \pi}{24}
\end{aligned}$
$\begin{aligned}
&\\
\qquad \cos (\angle A O B) &=\frac{10^{2}+10^{2}-15^{2}}{2(10)(10)} \\\\
&=-\frac{1}{8} \\\\
\angle A O B &=1.70 \text{ rad}\\\\
\end{aligned}$
$\begin{aligned}
\text{ (b) } \quad &\text{ The perpendicular distance from } O \text{ to } A B\\\\
&=\sqrt{10^{2}-\left(\frac{15}{2}\right)^{2}} \\\\
&=6.61\\\\
\therefore\ & \text{ The perpendicular distance from } C \text{ to } A B\\\\
&=25-6.61 \\\\
&=18.39\\\\
\end{aligned}$
$\begin{aligned}
& A C=B C=\sqrt{18.32^{2}+7.5^{2}} \\\\
&=19.86 \\\\
&\quad \text { length of major sector }\\\\
&=(2 \pi-1.7) \times 10 \\\\
&=45.83 \\\\
\therefore & \text { perimeter of shadld region } \\\\
=&\ 2(19.8 b)+45.83 \\\\
=&\ 85.55\\\\
\end{aligned}$
$\begin{aligned}
&\quad \text{ area of major sector }\\\\
&=\frac{1}{2} \times 10^{2}(2 \pi-1.7) \\\\
&=229.15 \\\\
&\quad \text { area of kite AOBC } \\\\
&= \frac{1}{2} \times 25 \times 15 \\\\
&=187.5 \\\\
&=229.15+187.55 \\\\
&=416.65
\end{aligned}$

Post a Comment for "May-Jun-21-p1-CIE-0606/11 : Solution"