Oct-Nov-21-p1-CIE-0606/11 : Solution
2021 CIE (Additional Mathematics), Paper 1 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။
The diagram shows the graph of $y=a \sin \dfrac{x}{b}+c$ for
$-360^{\circ} \le x \le 360^{\circ}$,
(a) Write down the period of $a \sin \dfrac{x}{b}+c$.
[1]
(b) Find the value of $a$, of $b$ and of $c$.
[3]
Points $A$ and $C$ have coordinates $(-4, 6)$ and $( 2, 18)$ respectively.
The point $B$ lies on the line $A C$ such that
$\overrightarrow{A B}=\dfrac{2}{3} \overrightarrow{A C}$.
(a) Find the coordinates of $B$.
[2]
(a) Find the equation of the line $l$, which is perpendicular
to $AC$ and passes through B.
[2]
(c) Find the area enclosed by the line $l$ and the coordinate axes.
[2]
(a) Find the vector which has magnitude $39$ and is in the same direction as
$\left(\begin{array}{r}12 \\ -5\end{array}\right)$.
[2]
(b) Given that $\mathbf{a}=\left(\begin{array}{r}
2 \\
-1
\end{array}\right)$ and $\mathbf{b}=\left(\begin{array}{r}
-4 \\
5
\end{array}\right)$, find the constants $\lambda$ and $\mu$ such that $5 \mathbf{a}+\lambda\left(\begin{array}{l}
4 \\
6
\end{array}\right)=\mu \mathbf{b}$
[4]
SOLUTION
(a) Given that $\dfrac{q^{-2} \sqrt{p r}}{\sqrt[3]{r}(p q)^{-3}}=p^{a} q^{b} r^{c}$,
find the value of each of the constants $a, b$ and $c$.
[3]
(b) Solve the equation $3 x^{\frac{4}{5}}-8 x^{\frac{2}{5}}+5=0$.
[4]
SOLUTION
The polynomial $\mathrm{p}(x)=a x^{3}+b x^{2}+6 x+4$, where $a$ and $b$ are integers,
is divisible by $x-2$. When $\mathrm{p}^{\prime}(x)$ is divided by $x+1$ the remainder is $-7$.
(a) Find the value of $a$ and of $b$.
[5]
(b) Using your answers to part (a), find the remainder when
$\mathrm{p}^{\prime \prime}(x)$ is divided by $x$.
[2]
SOLUTION
A curve with equation $y=f(x)$ is such that
$\dfrac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}=6 \mathrm{e}^{3 x}+4 x$.
The curve has a gradient of 5 at the point $\left(0, \dfrac{5}{3}\right)$. Find $f(x)$.
[7]
The first three terms, in ascending powers of $x$, in the expansion
of $(2+a x)^{n}$ can be written as $64+b x+c x^{2}$, where $n, a, b$ and $c$ are constants.
(a) Find the value of $n$.
[1]
(b) Show that $5 b^{2}=768 c$.
[4]
(c) Given that $b = 12$, find the exact value of $a$ and of $c$.
[2]
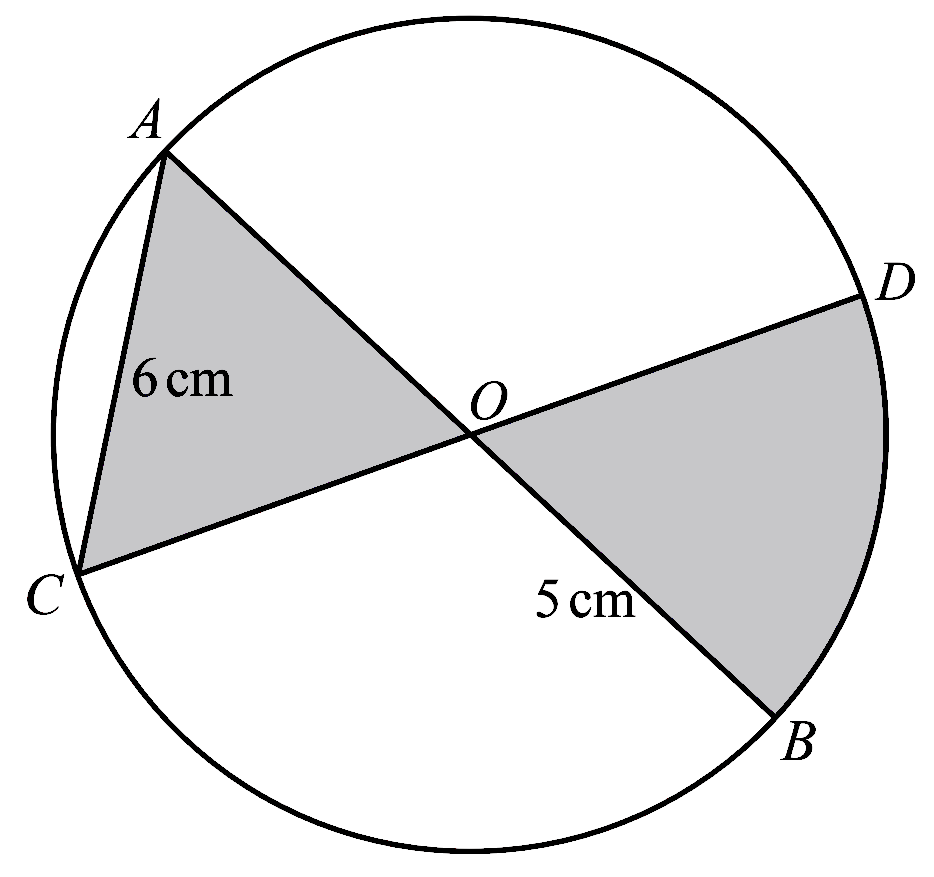
The diagram shows a circle, centre $O$, radius $5$ cm. The lines $AOB$ and $COD$ are
diameters of this circle. The line $AC$ has length $6$ cm.
(a) Show that angle $AOC = 1.287$ radians, correct to $3$ decimal places.
[2]
(b) Find the perimeter of the shaded region.
[2]
(c) Find the area of the shaded region.
[3]
(a) Find the coordinates of the stationary points on the curve
$y=(2 x+1)(x-3)^{2}$. Give your answers in exact form.
[4]
(b) On the axes below, sketch the graph of $y=\left|(2 x+1)(x-3)^{2}\right|,$
stating the coordinates of the points where the curve meets the axes.
[4]
(c) Hence write down the value of the constant $k$ such that
$\left|(2 x+1)(x-3)^{2}\right|=k $ has exactly 3 distinct solutions.
[1]
SOLUTION
(a) Jess runs on 5 days each week to prepare for a race.
In week 1 , every run is $2$ km.
In week 2, every run is $2.5 $ km.
In week 3 , every run is $3 $ km.
Jess increases the distance of the run by $0.5 $ km every week.
(i) Find the week in which Jess runs $16 $ km on each of the $5$ days.
[3]
(ii) Find the total distance Jess will have run by the end of week $8$.
[3]
(b) Kyle also runs on 5 days each week to prepare for a race.
In week 1 , every run is $2 $ km.
In week 2, every run is $2.5 $ km.
In week 3, every run is $3.125 $ km.
The distances he runs each week form a geometric progression.
(i) Find the common ratio of the geometric progression.
[3]
(ii) Find the first week in which Kyle will run more than $16$ km on each of the $5$ days.
[3]
(iii) Find the total distance Kyle will have run by the end of week $8$.
[3]
SOLUTION
(a) Solve the equation
$3 \operatorname{cosec}^{2} \theta-5=5 \cot \theta$ for $0^{\circ} \le \theta \le180^{\circ}$.
[4]
(b) Solve the equation $\sin \left(\phi+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}$,
where $\phi$ is in radians and $-\pi \le \phi \le \pi$. Give your answers
in terms of $\pi$.
[4]
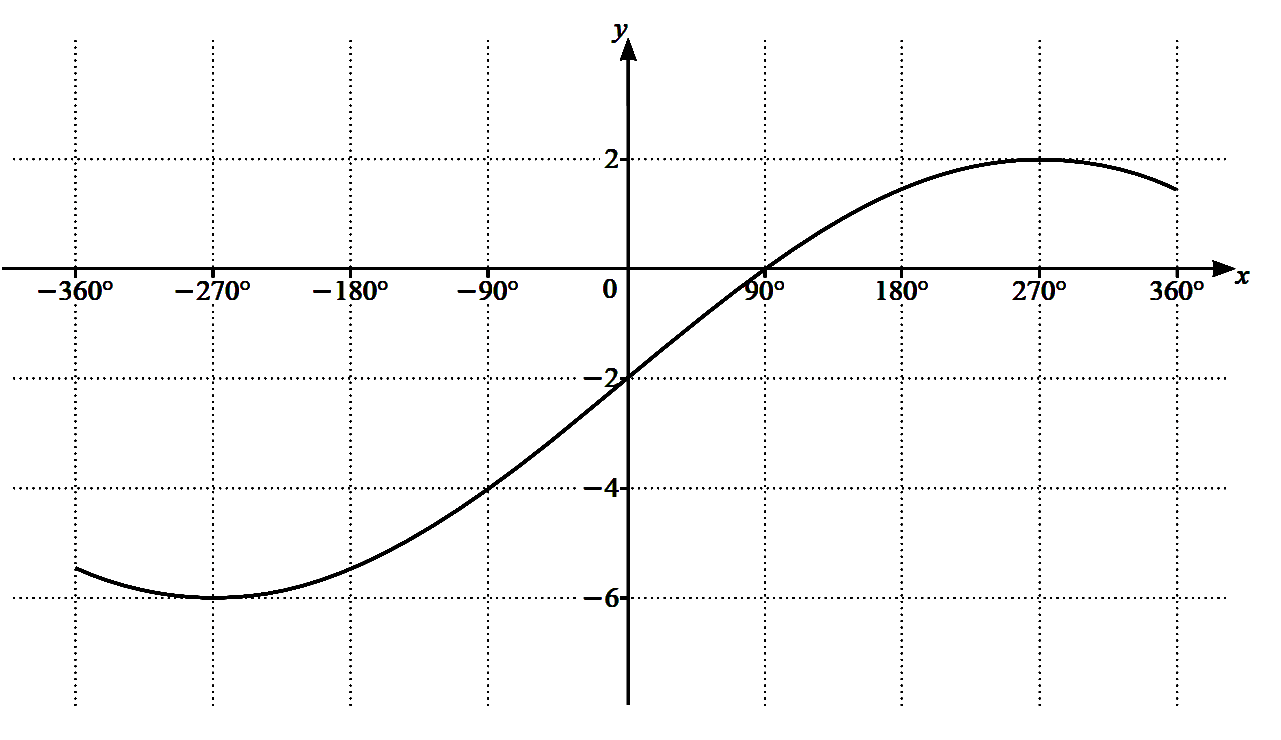
SOLUTION
$\begin{aligned}
\text{(a)}\quad \frac{1}{4} \text{ period }&=270^{\circ}\\\\
1 \text{ period } &=270^{\circ} \times 4\\\\
&=1080^{\circ}\\\\
\end{aligned}$
$\begin{aligned}
\text{(b)}\quad &-1 \le \sin \frac{x}{b} \le 1 \\\\
&-a \le a \sin \frac{x}{b} \le a \\\\
&-a+c \le a \sin \frac{x}{b}+c \le a+c\\\\
\therefore\ &-a+c=-6 \quad \ldots(1)\\\\
\end{aligned}$
$\begin{aligned}
a+c &=2 \ldots(2) \\\\
\text{By } (1) &+(2), \\\\
2 c &=-4 \\\\
c &=-2 \\\\
\text{By } (2) &-(1), \\\\
2 a &=8 \\\\
a &=4\\\\
\text{When } x&=90^{\circ},\\\\
a \sin \frac{x}{b}+c&=0\\\\
4 \sin \frac{90^{\circ}}{b}-2&=0\\\\
\sin \frac{30^{\circ}}{b}&=\frac{1}{2}\\\\
\frac{90^{\circ}}{b}&=30^{\circ}\\\\
\therefore\ b&=3
\end{aligned}$
SOLUTION
$\begin{aligned}
\text{ (a) } \quad \overrightarrow{O A} &=\left(\begin{array}{c}
-4 \\\\
6
\end{array}\right) \\\\
\overrightarrow{O C} &=\left(\begin{array}{c}
2 \\\\
18
\end{array}\right) \\\\
\text { Let } \overrightarrow{O B} &=\left(\begin{array}{l}
x \\\\
y
\end{array}\right) \\\\
\overrightarrow{A B} &=\overrightarrow{O B}-\overrightarrow{O A} \\\\
&=\left(\begin{array}{l}
x \\\\
y
\end{array}\right)-\left(\begin{array}{c}
-4 \\\\
6
\end{array}\right) \\\\
&=\left(\begin{array}{l}
x+4 \\\\
y-6
\end{array}\right)\\\\
\overrightarrow{A C} &=\overrightarrow{O C}-\overrightarrow{O A} \\\\
&=\left(\begin{array}{c}
2 \\\\
18
\end{array}\right)-\left(\begin{array}{r}
-4 \\\\
6
\end{array}\right) \\\\
&=\left(\begin{array}{c}
6 \\\\
12
\end{array}\right) \\\\
\overrightarrow{A B} &=\dfrac{2}{3} \overrightarrow{A C} \\\\
\left(\begin{array}{c}
x+4 \\\\
y-6
\end{array}\right) &=\dfrac{2}{3}\left(\begin{array}{c}
6 \\\\
12
\end{array}\right) \\\\
\left(\begin{array}{c}
x+4 \\\\
y-6
\end{array}\right) &=\left(\begin{array}{c}
4 \\\\
8
\end{array}\right)\\\\
\therefore x+4 &=4 \\\\
x &=0 \\\\
y-6 &=8 \\\\
y &=14 \\\\
\end{aligned}$
$\therefore$ The point $B$ is $(8,14)$.
$\text{ (a) }$ Let the gradient (slope) of $A C$ be $m_{A C}.$
$\begin{aligned}
&\\
&\therefore m_{A C}=\dfrac{18-6}{2-(-4)}=\dfrac{12}{6}=2 \\\\
&l \perp A C \\\\
&\therefore m_{l}=-\dfrac{1}{2}\\\\
\end{aligned}$
$\therefore$ Equation of the line l is
$\begin{aligned}
&\\
y-14&=-\dfrac{1}{2}(x-0)\\\\
y&=-\dfrac{1}{2} x+14\\\\
\end{aligned}$
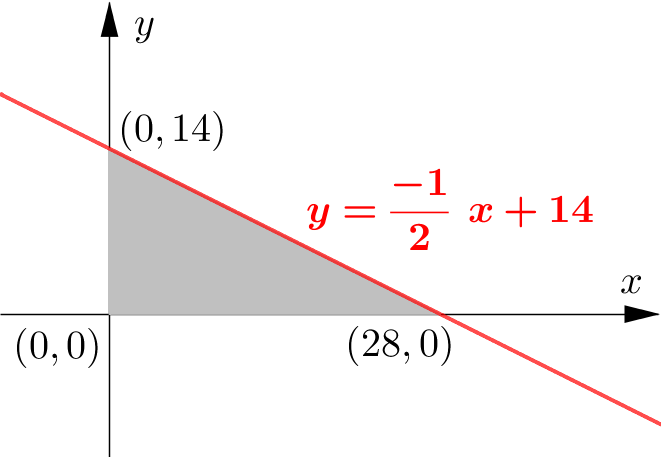
$\text{ (c) }$ When $x=0, y=14\\\\ $.
$\therefore\ l$ cuts $y$-axis at $(0,14).\\\\ $
When $y=0, x=28\\\\ $
$\therefore\ l$ cuts $x$-axis at $(28,0).\\\\ $
The area enclosed by $l$ and coordinate axes is
$\begin{aligned}
&\\
A &=\dfrac{1}{2} \times 28 \times 14 \\\\
&=196 \text { sq-units. }
\end{aligned}$
$\text {(a) }\quad$ Let $\vec{a}=\left(\begin{array}{c}12 \\\\ -5\end{array}\right).$
$\begin{aligned}
&\\
\therefore\ |\vec{a}| &=\sqrt{12^{2}+(-5)^{2}} \\\\
&=\sqrt{169} \\\\
&=13 \\\\
\therefore\ \quad \hat{a} &=\frac{\vec{a}}{|\vec{a}|} \\\\
&=\frac{1}{13}\left(\begin{array}{l}
12 \\\\
-5
\end{array}\right)
\end{aligned}$
Let the required vector be $\vec{b}$.
$\begin{aligned}
&\\
\therefore\ |\vec{b}|=39 \text { (given) }
\end{aligned}$
Since $\vec{b}$ is in the same direction as $\vec{a}$.
$\begin{aligned}
&\\
\vec{b} &=|\vec{b}| \hat{a} \\\\
&=39 \times \frac{1}{13}\left(\begin{array}{c}
12 \\\\
-5
\end{array}\right) \\\\
&=\left(\begin{array}{c}
36 \\\\
-15
\end{array}\right)\\\\
\end{aligned}$
$\begin{aligned}
\text {(b) } \quad &\vec{a}=\left(\begin{array}{c}
2 \\\\
-1
\end{array}\right) \\\\
&\vec{b}=\left(\begin{array}{c}
-4 \\\\
5
\end{array}\right) \\\\
&5 \vec{a}+\lambda\left(\begin{array}{c}
4 \\\\
6
\end{array}\right)=\mu b \\\\
&5\left(\begin{array}{c}
2 \\\\
-1
\end{array}\right)+\lambda\left(\begin{array}{c}
4 \\\\
6
\end{array}\right)=\mu\left(\begin{array}{c}
-4 \\\\
5
\end{array}\right) \\\\
&\left(\begin{array}{c}
10 \\\\
-5
\end{array}\right)+\left(\begin{array}{c}
4 \lambda \\\\
6 \lambda
\end{array}\right)=\left(\begin{array}{c}
-4 \mu \\\\
5 \mu
\end{array}\right) \\\\
&\left(\begin{array}{c}
10+4 \lambda \\\\
-5+6 \lambda
\end{array}\right)=\left(\begin{array}{c}
-4 \mu \\\\
5 \mu
\end{array}\right)\\\\
\end{aligned}$
$\begin{aligned}
\therefore\ 10+4 \lambda &=-4 \mu \\\\
\therefore\ \mu &=\frac{-(5+2 \lambda)}{2} \\\\
-5+6 \lambda &=5 \mu \\\\
-5+6 \lambda &=\frac{-5(5+2 \lambda)}{2} \\\\
-10+12 \lambda &=-25-10 \lambda \\\\
22 \lambda &=-15 \\\\
\lambda &=-\frac{15}{22} \\\\
\mu &=-\frac{1}{2}\left(5+2\left(-\frac{15}{22}\right)\right) \\\\
&=-\frac{20}{11}
\end{aligned}$
$\begin{aligned}
\text{ (a) } \hspace{2.5cm} \frac{q^{-2} \sqrt{p r}}{\sqrt[3]{r}(p q)^{-3}} &=p^{a} q^{b} r^{c} \\\\
\frac{q^{-2} p^{\frac{1}{2}} r^{\frac{1}{2}}}{r^{\frac{1}{3}} p^{-3} q^{-3}} &=p^{a} q^{b} r^{e} \\\\
(p)^{\frac{1}{2}+3} (q)^{-2+3} (r)^{\frac{1}{2}-\frac{1}{3}} &=p^{a} q^{b} r^{e} \\\\
p^{\frac{7}{2}} q r^{\frac{1}{6}} &=p^{a} q^{b} r^{e}\\\\
\therefore a &=\frac{7}{2} \\\\
b &=1 \\\\
c &=\frac{1}{6}\\\\
\end{aligned}$
$\begin{aligned}
\text{ (b) } \hspace{2cm} 3 x^{\frac{4}{5}}-8 x^{\frac{2}{5}}+5 &=0 \\\\
3\left(x^{2 / 5}\right)^{2}-8 x^{2 / 5}+5&=0 \\\\
\left(3 x^{2 / 5}-5\right)\left(x^{2 / 5}-1\right)&=0 \\\\
x^{2 / 5}=\frac{5}{3} \text { (or) } x^{2 / 5}&=1 \\\\
x=\left(\frac{5}{3}\right)^{5 / 2} \text { (or) } x&=7
\end{aligned}$
$\begin{aligned}
&p(x)=a x^{3}+b x^{2}+6 x+4 \\\\
&p^{\prime}(x)=3 a x^{2}+2 b x+6 \\\\
&p(x) \text { is divisible by } x-2, \\\\
\therefore\ & p(2)=0 \\\\
&8 a+4 b+12+4=0 \\\\
&2 a+b=-4 \\\\
&b=-2 a-4 \\\\
&\text { When } p^{\prime}(x) \text { is divided by }(x+1),\\\\
& p(x)=a x^{3}+b x^{2}+6 x+4 \\\\
& p^{\prime}(x)=3 a x^{2}+2 b x+6 \\\\ & p(x) \text { ie divisible by } x-2, \\\\
\therefore\ & p(2)=0 \\\\
& 8 a+4 b+12+4=0 \\\\
& 2 a+b=-4 \\\\
& b=-2 a-4 \\\\
& \text { When } p^{\prime}(x) \text { is divided by }(x+1) \\\\
& \text { the remainder is - } 7 . \\\\
\therefore\ & p(-1)=-7 \\\\
& 3 a-2 b+6=-7\\\\
& 3 a-2 b=-13 \\\\
& 3 a-2(-2 a-4)=-13 \\\\
& 3 a+4 a+8=-13 \\\\
& 7 a=-21 \\\\
& a=-3 \\\\
\therefore \ & b=-2(-3)-4 \\\\
& b=2 \\\\
\therefore \ & p^{\prime}(x)=-9 x^{2}+4 x+6 \\\\
\therefore \ & p^{\prime \prime}(x)=-18 x+4\\\\
\end{aligned}$
When $p^{\prime \prime}(x)$ is divided by $x$,
$\begin{aligned}
&\\
\text{ the remainder } &=p^{\prime \prime}(0)\\\\
&=-18(0)+4 \\\\
&=4
\end{aligned}$
SOLUTION
$\begin{aligned}
y &=f(x) \\\\
\frac{d^{2} y}{d x^{2}} &=6 e^{3 x}+4 x \\\\
\therefore\ \frac{d y}{d x} &=\displaystyle\int\left(6 e^{3 x}+4 x\right) d x \\\\
&=6 \displaystyle\int e^{3 x} d x+4 \displaystyle\int x d x \\\\
&=\frac{6}{3} e^{3 x}+\frac{4}{2} x^{2}+c_{1} \\\\
&=2\left(e^{3 x}+x^{2}\right)+c_{1}\\\\
\end{aligned}$
The curve has gradient of 5 at the point $\left(0, \dfrac{5}{3}\right)$.
$\begin{aligned}
&\\
\therefore\ {{\left. {\frac{{dy}}{{dx}}} \right|}_{{\left( {0,\frac{5}{3}} \right)}}}&=5 \\\\
2\left(e^{0}+0\right)+c_{1} &=5 \\\\
\therefore\ c_{1} &=3 \\\\
\therefore\ \frac{d y}{d x} &=2 e^{3 x}+2 x^{2}+3\\\\
\therefore\ y &=\displaystyle\int\left(2 e^{3 x}+2 x^{2}+3\right) d x \\\\
&=2 \displaystyle\int e^{3 x} d x+2 \displaystyle\int x^{2} d x+3 \displaystyle\int d x \\\\
&=\frac{2}{3} e^{3 x}+\frac{2}{3} x^{3}+3 x+c_{2}\\\\
\end{aligned}$
Since $\left(0, \dfrac{5}{3}\right)$ lies on the curve,
$\begin{aligned}
&\\
\frac{5}{3} &=\frac{2}{3} e^{0}+\frac{2}{3}(0)^{3}+3(0)+c_{2} \\\\
\therefore\ c_{2} &=1 \\\\
\therefore\ f(x) &=\frac{2}{3} e^{3 x}+\frac{2}{3} x^{3}+3 x+7
\end{aligned}$
SOLUTION
$\begin{aligned}
&(2+a x)^{n}=64+b x+c x^{2}+\cdots \\\\
&2^{n}+n 2^{n-1}(a x)+\frac{n(n-1)}{2} 2^{n-2}(a x)^{2}=64+b x+c x^{2}+\cdots \\\\
\therefore \quad &2^{n}=64 \\\\
&2^{n}=2^{6} \\\\
&n=6 \\\\
\therefore \quad & 6\left(2^{5}\right)(a x)=b x \\\\
\therefore \quad & b=192 a \\\\
&a=\frac{b}{192}\\\\
\end{aligned}$
$\begin{aligned}
\frac{6 \times 5}{2} \times 2^{4} a^{2} x^{2} &=c x^{2} \\\\
240 a^{2} x^{2} &=c x^{2} \\\\
c &=240 a^{2} \\\\
\therefore \quad c &=240\left(\frac{b}{192}\right)^{2} \\\\
\therefore \quad 5 b^{2} &=768 c\\\\
b &=12\quad \text { (given) } \\\\
\therefore a &=\frac{12}{192} \\\\
&=\frac{1}{16} \\\\
c &=\frac{5 \times 12^{2}}{768} \\\\
&=\frac{15}{16}
\end{aligned}$
SOLUTION
By cosine rule,
$\begin{aligned}
&\\
\cos (\angle A O C) &=\frac{5^{2}+5^{2}-6^{2}}{2 \times 5 \times 5} \\\\
&=\frac{7}{25} \\\\
\angle A O C &=\cos ^{-1}\left(\frac{7}{25}\right) \\\\
\therefore\ \angle B O D &=1.287\quad \mathrm{rad}\\\\
\end{aligned}$
length of arc $B D=O B\times\angle B O D$
$\begin{aligned}
&\\
&=5(1.287) \\\\
&=6.44\\\\
\end{aligned}$
$\begin{aligned}
&\quad \text{perimeter of shaded regron}\\\\
&=A C+\operatorname{arc} B D+A B+C D \\\\
&=6+6.44+10+10 \\\\
&=32.44 \\\\
&=32.4 \text { (3~sff) }\\\\
\end{aligned}$
$\begin{aligned}
&\quad \text {area of } \triangle A O C\\\\
&=\frac{1}{2} O C \sin (\angle A O C) \times O A \\\\
&=\frac{1}{2}(5) \sin (1.287) \times 5 \\\\
&=12 \\\\
&\quad \text {area of sector } BOD \\\\
&=\frac{1}{2} \times O B^{2}\times\angle B O D \\\\
&=\frac{1}{2}\left(5^{2}\right)(1.287) \\\\
&=16.1 \\\\
&\quad \text {area of shaded region } \\\\
&=12+16.1 \\\\
&=28.1
\end{aligned}$
$\begin{aligned}
\text{(a) }\quad y &=(2 x+1)(x-3)^{2} \\\\
\dfrac{d y}{d x} &=(2 x+1) \dfrac{d}{d x}(x-3)^{2}+(x-3)^{2} \dfrac{d}{d x}(2 x+1) \\\\
&=2(2 x+1)(x-3)+2(x-3)^{2} \\\\
&=2(x-3)(2 x+1+x-3) \\\\
&=2(x-3)(3 x-2) \\\\
\dfrac{d y}{d x} &=0 \text { when }\\\\
\end{aligned}$
$\begin{aligned}
\quad &2(x-3)(3 x-2)=0 \\\\
\quad &\therefore x=3 \text { or } x=\dfrac{2}{3} \\\\
\quad &\text { When } x=\dfrac{2}{3}, y=\dfrac{343}{27} \\\\
\quad &\text { When } x=3, y=0 \\\\
\end{aligned}$
$\therefore$ The stationary points are $\left(\dfrac{2}{3}, \dfrac{343}{27}\right)$ and $(3,0).$
$\begin{aligned}
&\\
\text{(b) } \hspace{1.5cm} \dfrac{d^{2} y}{d x^{2}} &=2\left[(x-3) \dfrac{d}{d x}(3 x-2)+(3 x-2) \dfrac{d}{d x}(x-3)\right] \\\\
\quad &=2[3 x-9+3 x-2] \\\\
\quad &=2(6 x-11) \\\\
\quad \left.\dfrac{d^{2} y}{d x^{2}}\right|_{\left(\dfrac{2}{3}, 0\right)} &=2\left(6 \times \dfrac{2}{3}-11\right)\\\\
\quad &=-14<0\\\\
\end{aligned}$
$\quad \therefore \quad \left(\dfrac{2}{3}, 0\right)$ is a minimum turning point.
$\begin{aligned}
&\\
\quad \left.\dfrac{d^{2} y}{d x^{2}}\right|_{(3,0)}&=2(6 \times 3-11)\\\\
\quad &=14>0
\end{aligned}$
$\quad \therefore\quad (3,0)$ is maximum turning point.
$\begin{aligned}
&\\
\quad \text{When } x=0, y=9\\\\
\quad \therefore\ y-\text{intercept } =(0,9)\\\\
\quad \text{When } y=0, x=-\dfrac{1}{2} \text{ or } x=3\\\\
\quad \therefore\ x-\text{intercept } =\left(-\frac{1}{2}, 0\right) \text{ and } (3,0)\\\\
\end{aligned}$
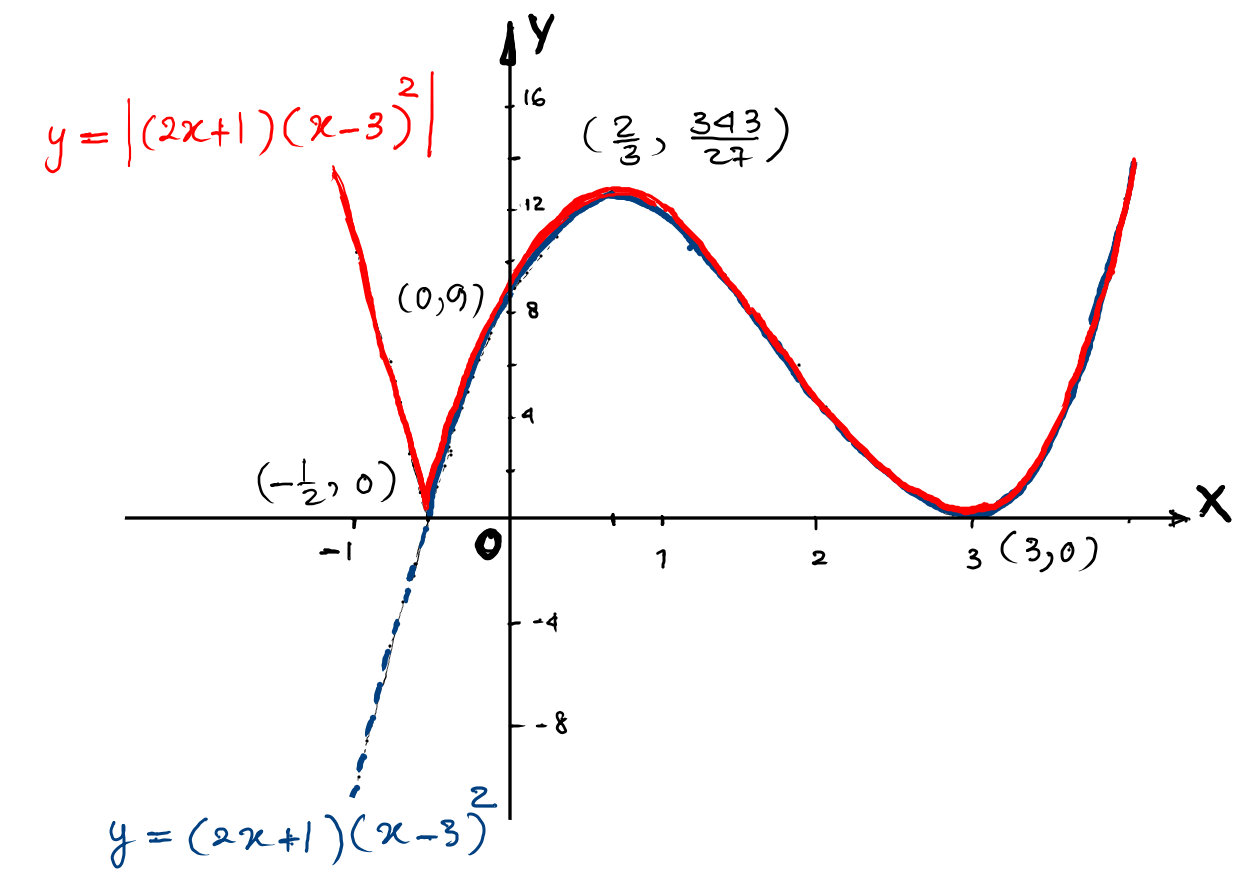
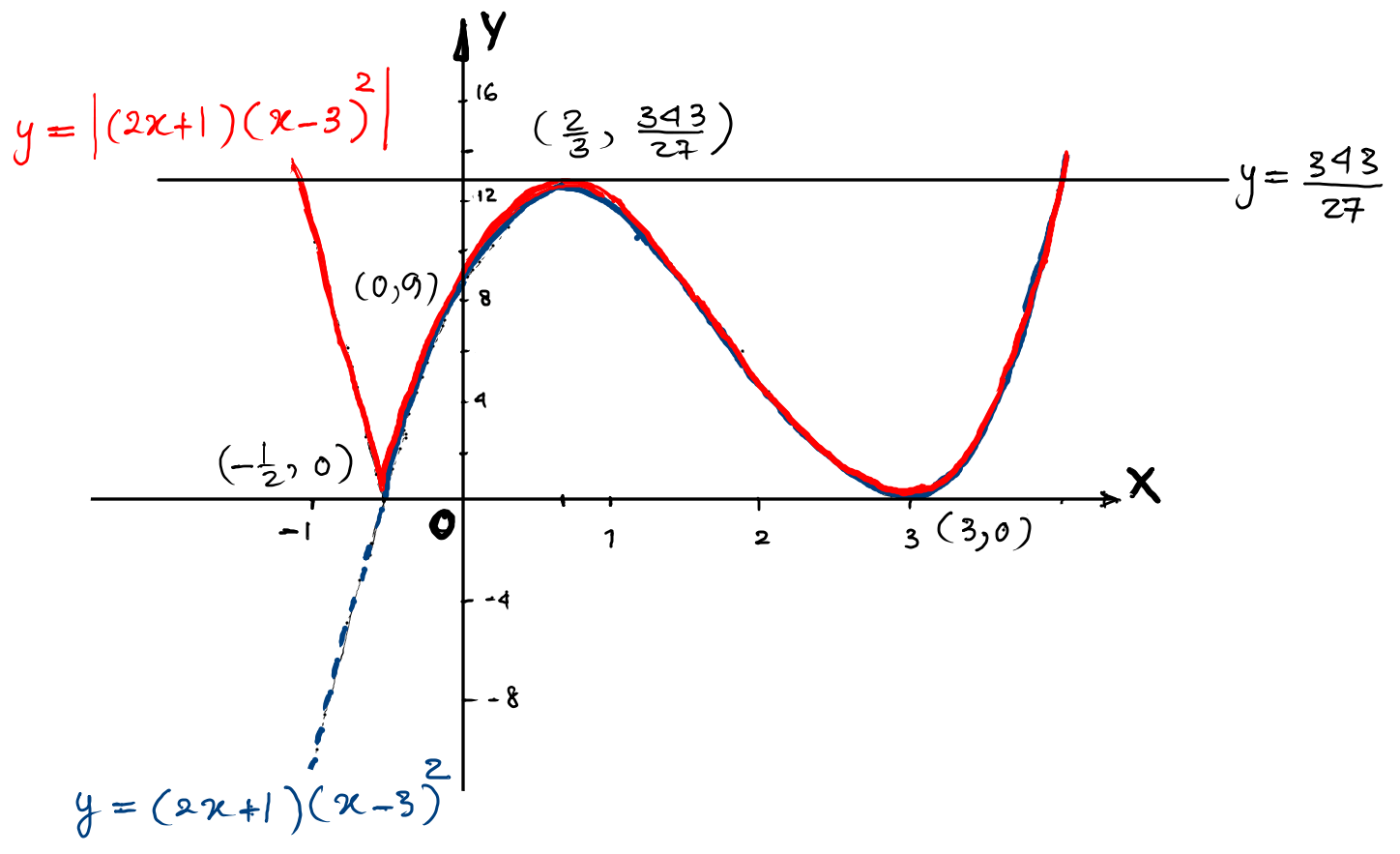
$\text{(c) } \quad \left|(2 x+1)(x-3)^{2}\right|=k$ has three distinct solutions.
This means that the graph of $y=k$ meets the graph
$y=\left|(2 x+1)(x-3)^{2}\right|$ at three distinct points.
By the diagram in part $(b)$, this condition is only possible when
$k=\dfrac{343}{27}$.
(a) Jeck runs on 5 days according to the following patterns.
$\begin{array}{|c|c|c|c|}
\hline \text{ week 1 } & \text{ week 2 } & \text{ week 3 } & \ldots \\
\hline 2 \mathrm{~km} \text{ a day } & 2.5 \mathrm{~km} \text{ a day } & 3 \mathrm{~km} \text{ a day } & \ldots \\
\hline
\end{array}$
This is an arithmetic progression with the first term $a=2$ and the common difference $d=0.5$.
(i) Assume that Jeck runs $16 \mathrm{~km}$ in week $n$.
$\begin{aligned}
&\\
\therefore \quad a+(n-1) d &=16 \\\\
2+(n-1) 0.5 &=16 \\\\
(n-1) 0.5 &=14 \\\\
n &=29\\\\
\end{aligned}$
Therefore, Jeck runs $16 \mathrm{~km}$ in week $29$ .
(ii) The total distance that Jecle will run by the end of week $8$ is
$\begin{aligned}
&\\
& \frac{8}{2} \times\{2(2)+7(0.5)\} \times 5 \\\\
=& 150 \text{ km}\\\\
\end{aligned}$
(b) Kyle runs on 5 days aecording to the following patterns.
$\begin{array}{|c|c|c|c|}
\hline \text{ week 1 } & \text{ week 2 } & \text{ week 3 } & \ldots \\
\hline 2 \mathrm{~km} \text{ a day } & 2.5 \mathrm{~km} \text{ a day } & 3.125 \mathrm{~km} \text{ a day } & \ldots \\
\hline
\end{array}$
The run of kyle on each week in in the form of geometric progression.
$\begin{aligned}
&\\
\text{(i) }\quad \therefore\ a &=2\\\\
r &=\frac{2 \cdot 5}{2} \\\\
&=1 \cdot 25\\\\
\end{aligned}$
(ii) Assume that Kyle runs $16 \mathrm{~km}$ in week $n$.
$\begin{aligned}
&\\
a r^{n-1} &>16 \\\\
2(1.25)^{n-1} &>16 \\\\
(1.25)^{n-1} &>8 \\\\
n-1 &>\frac{\ln 8}{\ln 1.25} \\\\
n-1 &>9.32 \\\\
n &>10.32 \\\\
\therefore\ n=11 \\\\
\end{aligned}$
Therefore The first week that Kyle runs more than $16 \mathrm{~km}$ is week 11.
(iii) The total distance Kyle will run by the end of week $8$ is
$\begin{aligned}
&\\
&\frac{2\left(1.25^{8}-1\right)}{1.25-1} \times 5 \\\\
&=198.42 \mathrm{~km}
\end{aligned}$
SOLUTION
$\begin{aligned}
\text{(a) } \quad 3 \operatorname{cosec}^{2} \theta-5&=5 \cot \theta, \quad 0^{\circ} \leq \theta \leq 180^{\circ}\\\\
3\left(1+\cot ^{2} \theta\right)-5 &=5 \cot \theta \\\\
3+3 \cot ^{2} \theta-5 &=5 \cot \theta \\\\
3 \cot ^{2} \theta-5 \cot \theta-2 &=0 \\\\
(3 \cot \theta+1)(\cot \theta-2) &=0 \\\\
\cot \theta =-\dfrac{1}{3} \text { or } \cot \theta&=2 \\\\
\theta=\left(180^{3}-4^{2} .56\right) \text { or } \theta &=26.56 \\\\
\theta=108.44^{\circ} \text { or } \theta &=26.56\\\\
\end{aligned}$
$\text{(b) } \quad \sin \left(\phi+\dfrac{\pi}{3}\right)=-\dfrac{1}{2},-\pi \leq \phi \leq \pi\\\\ $
basic acute angle (reference angle) $=\dfrac{\pi}{6}\\\\ $
$\sin \left(\phi+\dfrac{\pi}{3}\right)<0, \phi+\dfrac{\pi}{3}$ lies either $3^{r d}$ or $4^{\text {th }}$ quadrant.
$\begin{aligned}
&\\
\therefore \phi+\dfrac{\pi}{3}=\pi+\dfrac{\pi}{6} \quad \text { or } \quad \phi+\dfrac{\pi}{3} &=-\dfrac{\pi}{6} \\\\
\phi =\dfrac{5 \pi}{6} \quad \text { or } \quad \phi &=-\dfrac{\pi}{2}
\end{aligned}$

Post a Comment for "Oct-Nov-21-p1-CIE-0606/11 : Solution"