Transformation of Functions: Reflection

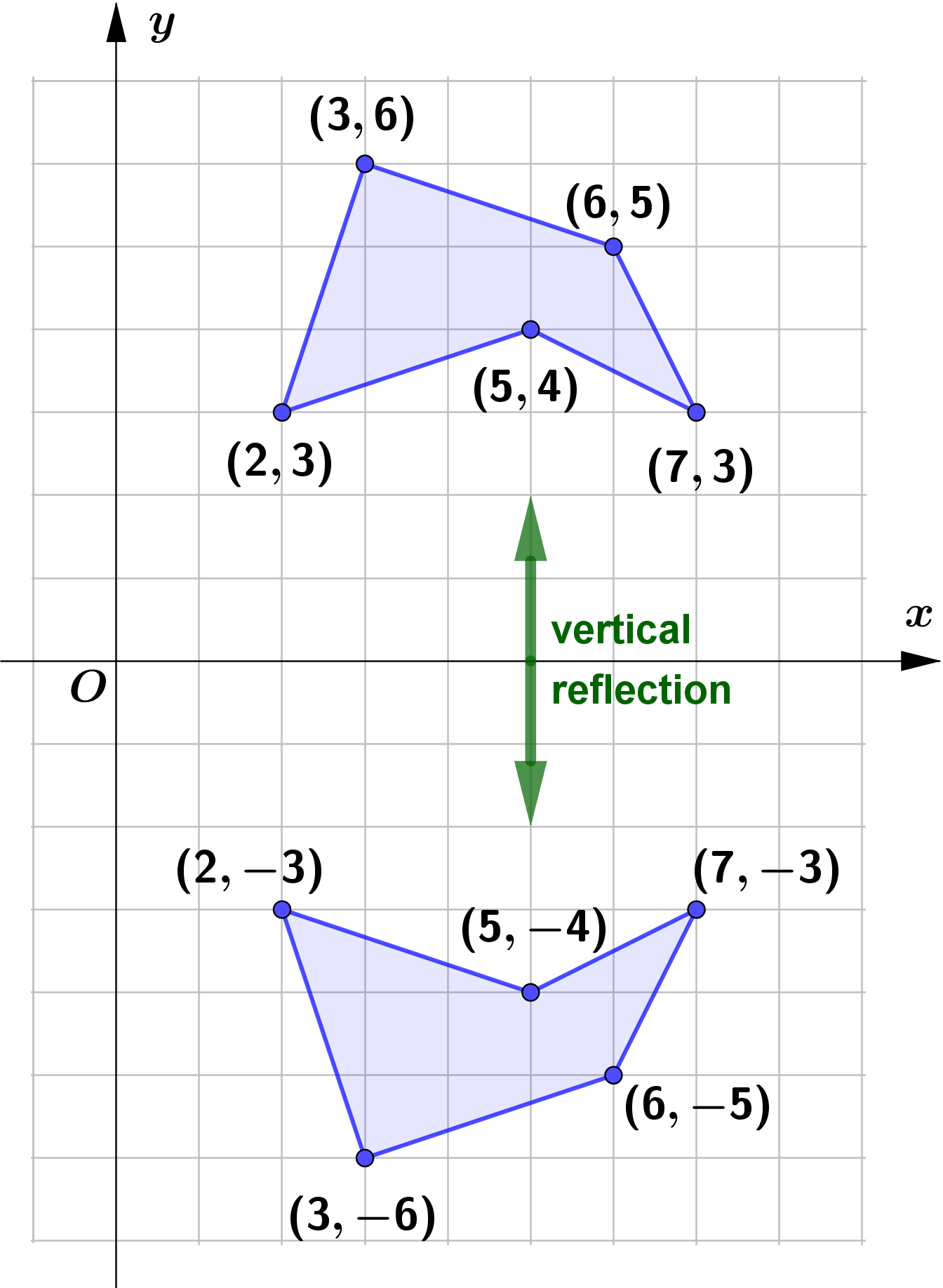
Vertical Reflection (Reflection about $x$-axis)

Given a function $f(x)$, a new function $g(x)=-f(x)$
is a horizontal reflection (reflection about the $x$-axis) of the function.

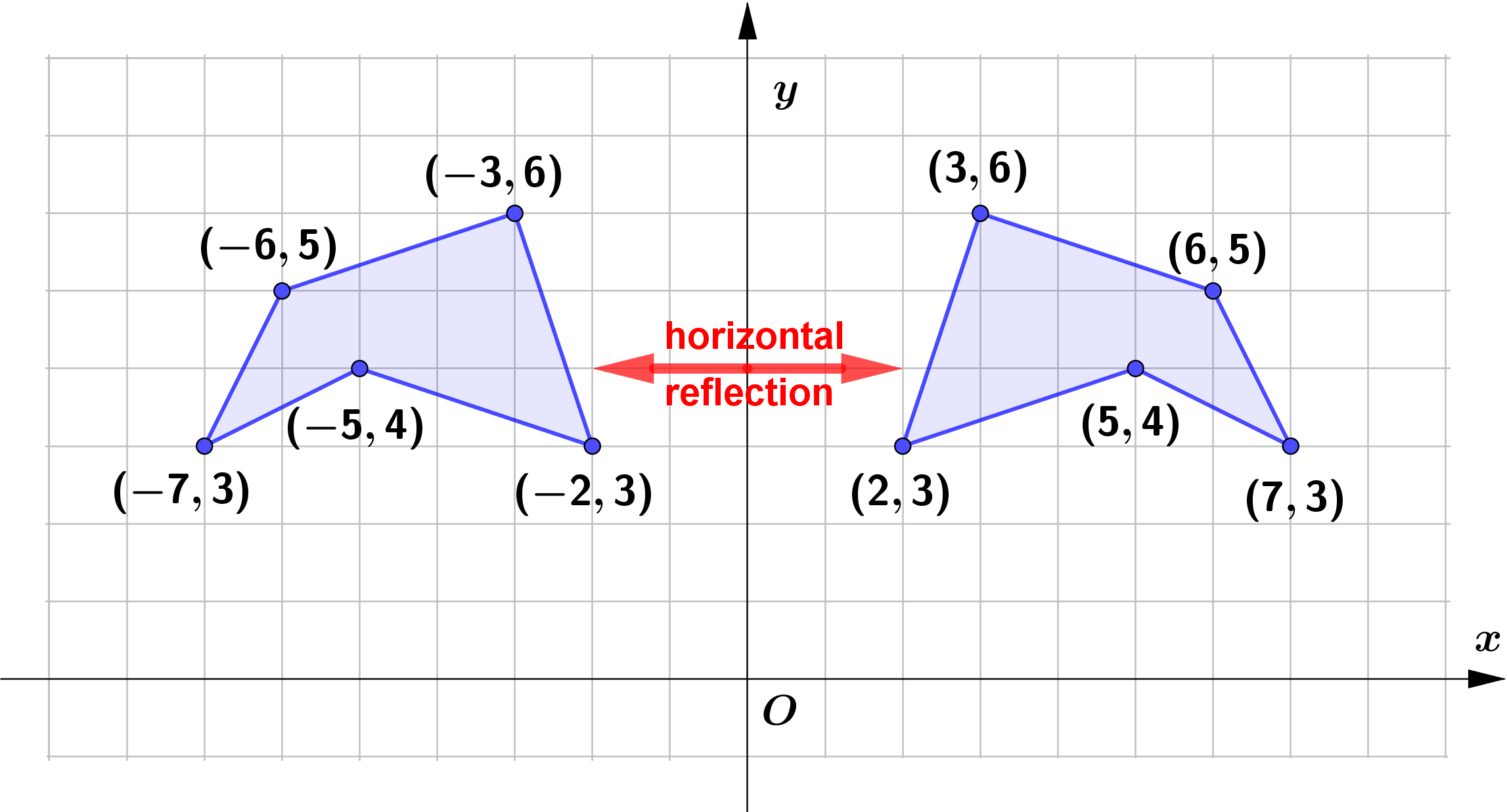
Horizontal Reflection (Reflection about $y$-axis)

Given a function $f(x)$, a new function $g(x)=-f(x)$
is a horizontal reflection (reflection about the $y$-axis) of the function.

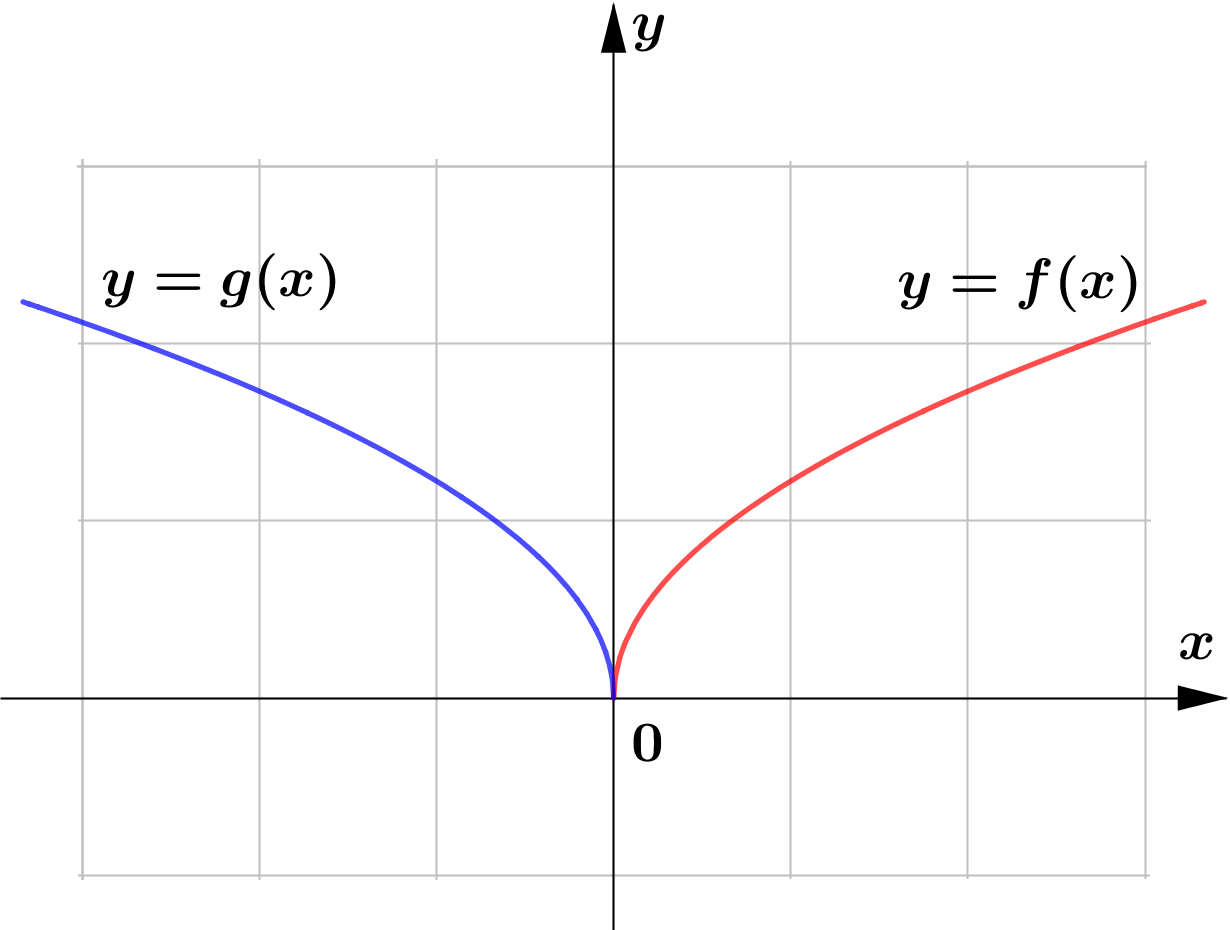
Question (1)

The following are the sketch of the graphs of $y=f(x)$ and $y=g(x)$. Determine whether the
graphs of $y=g(x)$ represents horizontal or vertical reflection of that of $y=f(x)$.

(a)

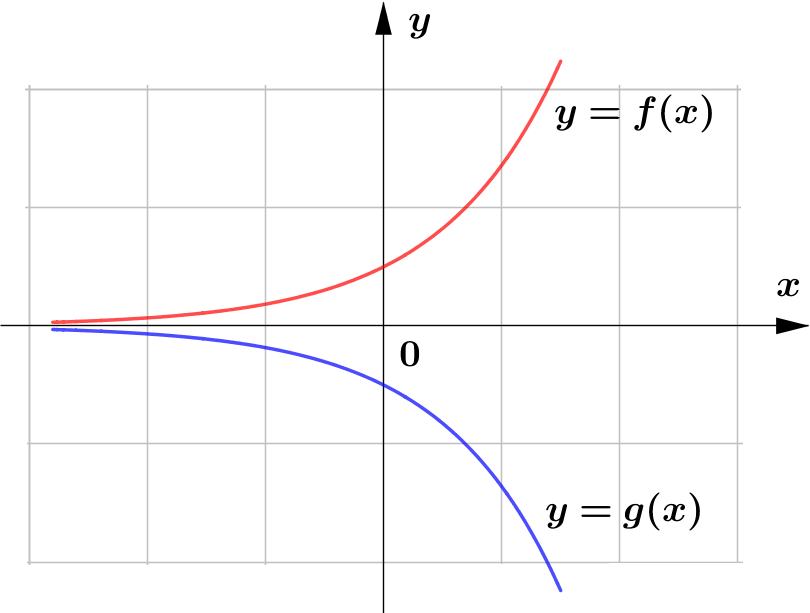
(b)

(c)

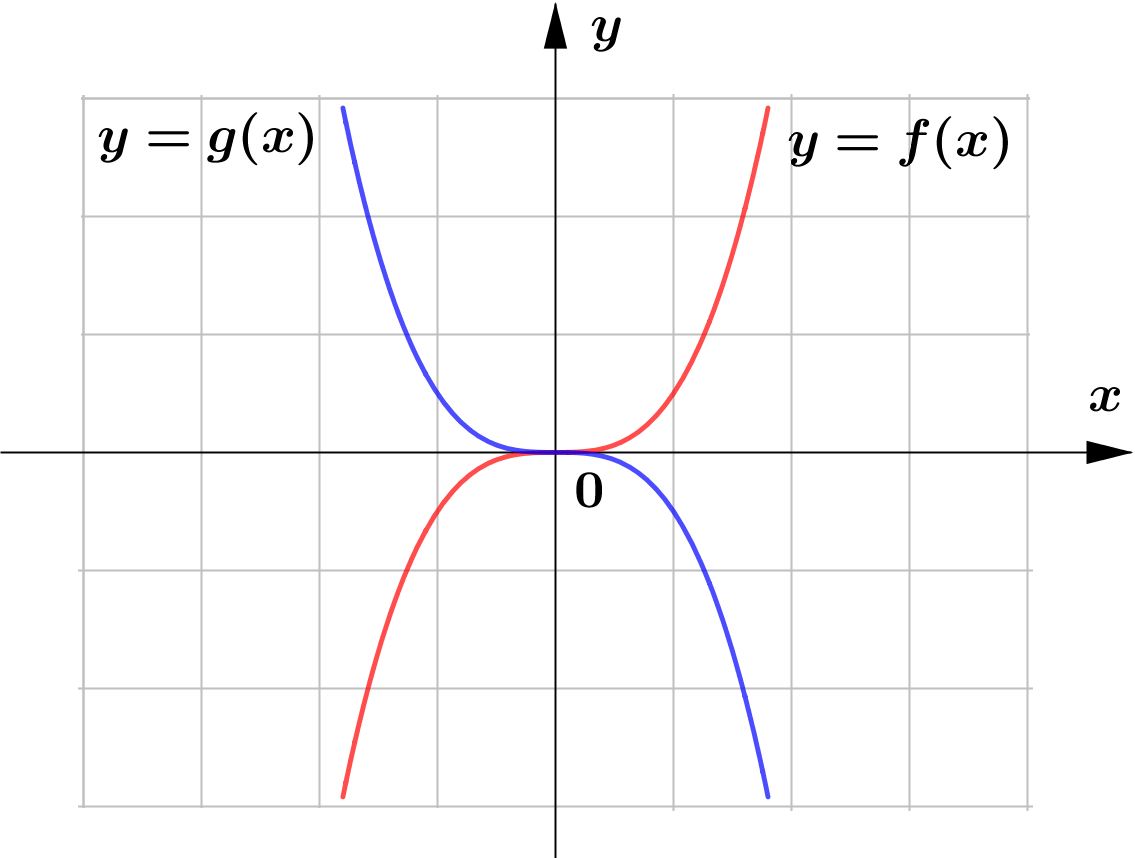
(d)

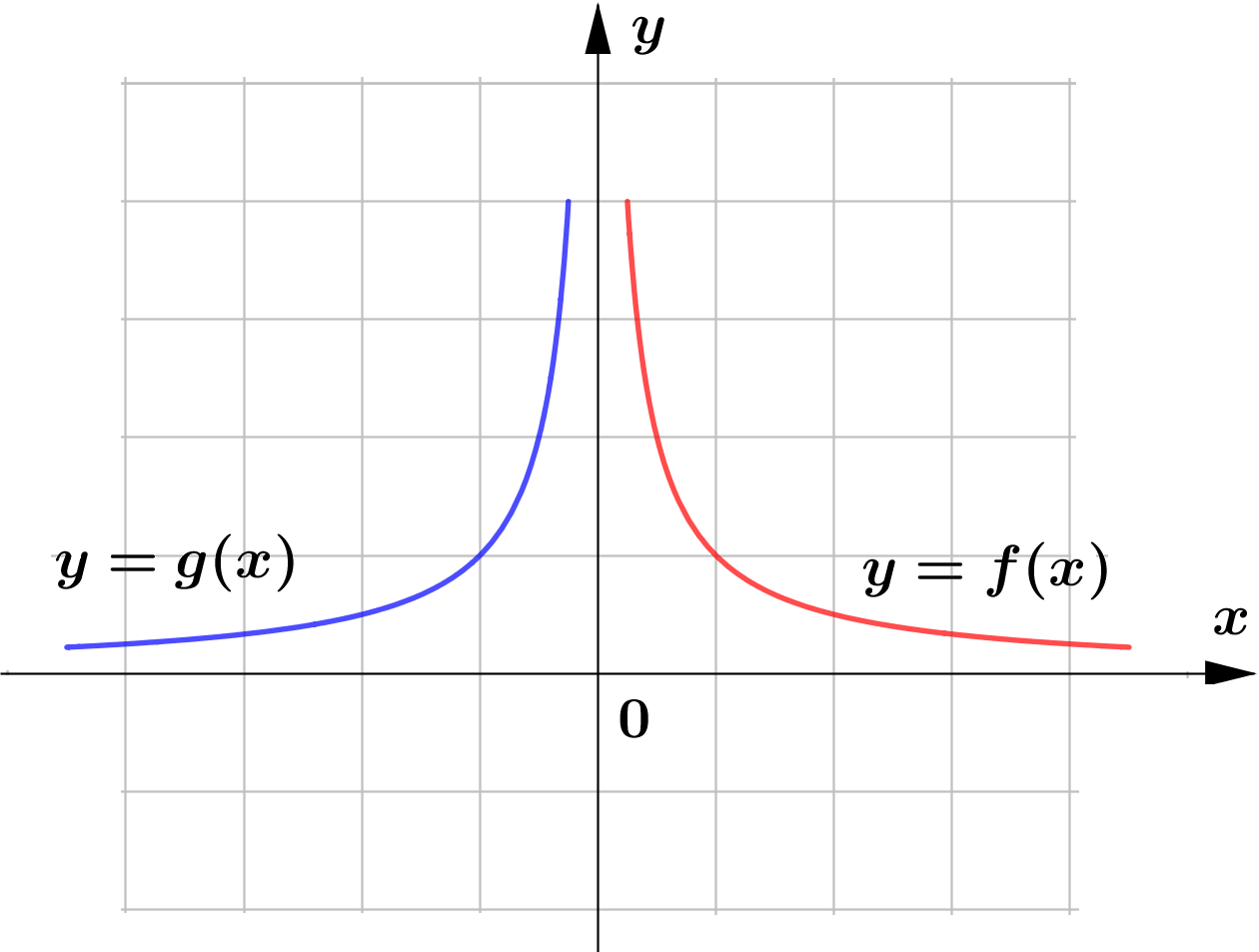
(e)

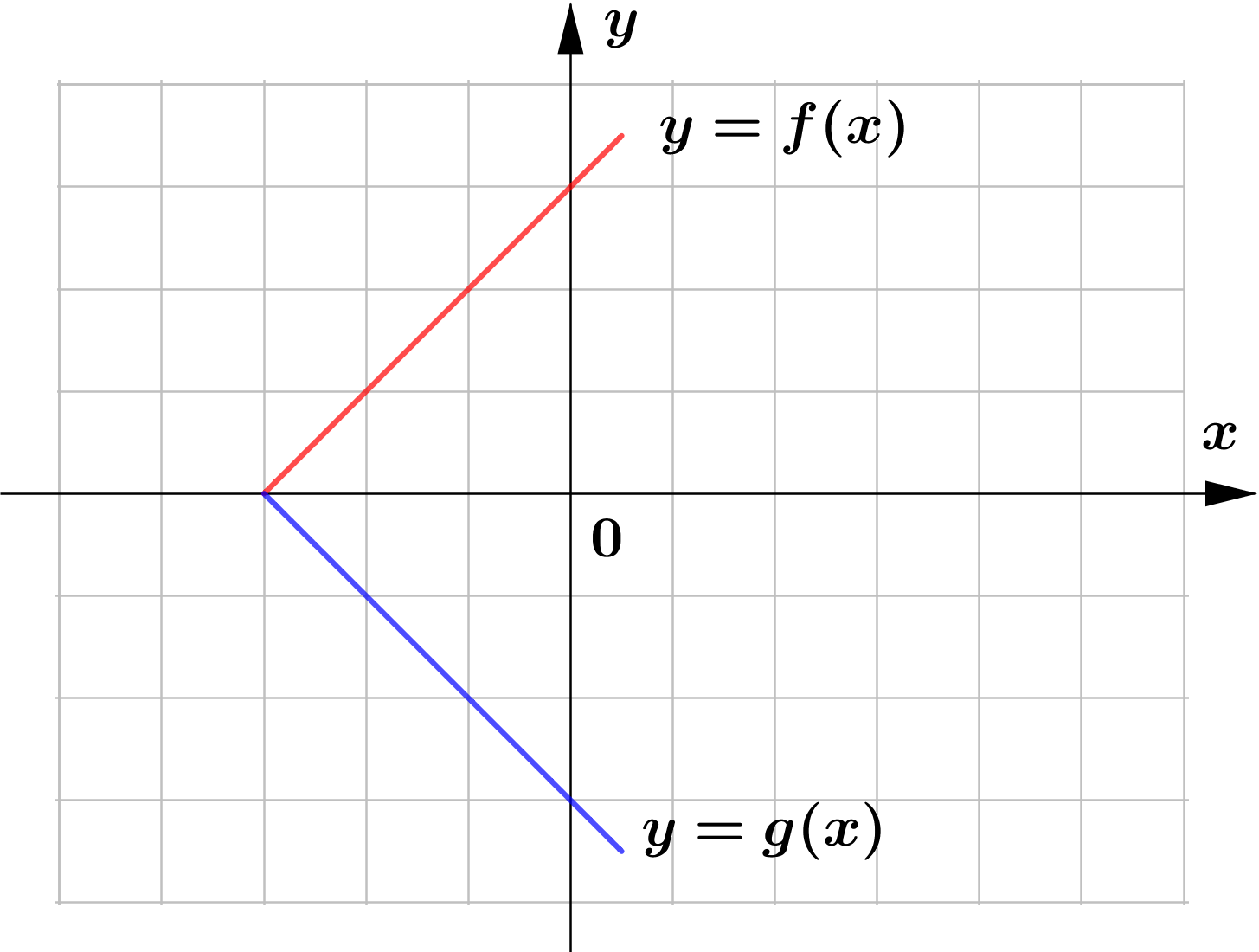
(f)

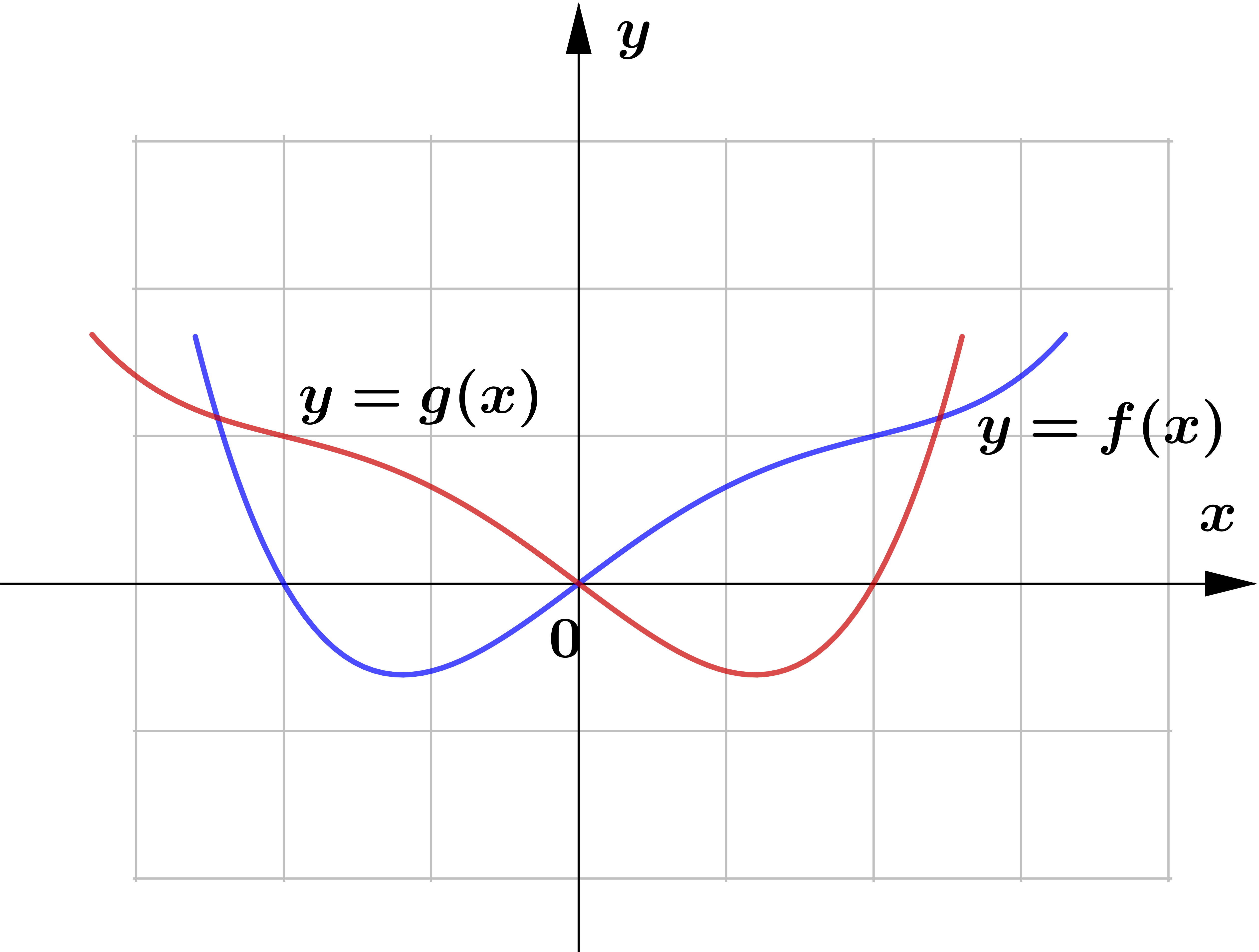
SOLUTION
$\text{(a) }$ horizontal reflection

$\text{(b) }$ vertical reflection

$\text{(c) }$ vertical reflection

$\text{(d) }$ horizontal reflection

$\text{(e) }$ vertical reflection

$\text{(f) }$ horizontalreflection

Question (2)

Assume that $(a, b)$ is a point on the graph of $y=f(x)$.
What is the corresponding point on the graph of each
of the following functions?

$\begin{array}{l}
\text{(a) } y=f(-x)\\\\
\text{(b) } y=-f(x)\\\\
\text{(c) } y=f(3-x)\\\\
\text{(d) } y=f(-x)-3
\end{array}$

SOLUTION
$\begin{array}{l}
\text{(a) }(-a, b)\\\\
\text{(b) } (a,-b)\\\\
\text{(c) } (3-a, b)\\\\
\text{(d) } (-a, b-3)
\end{array}$

Question (3)

The figure shows the graph of $y=h(x)$.

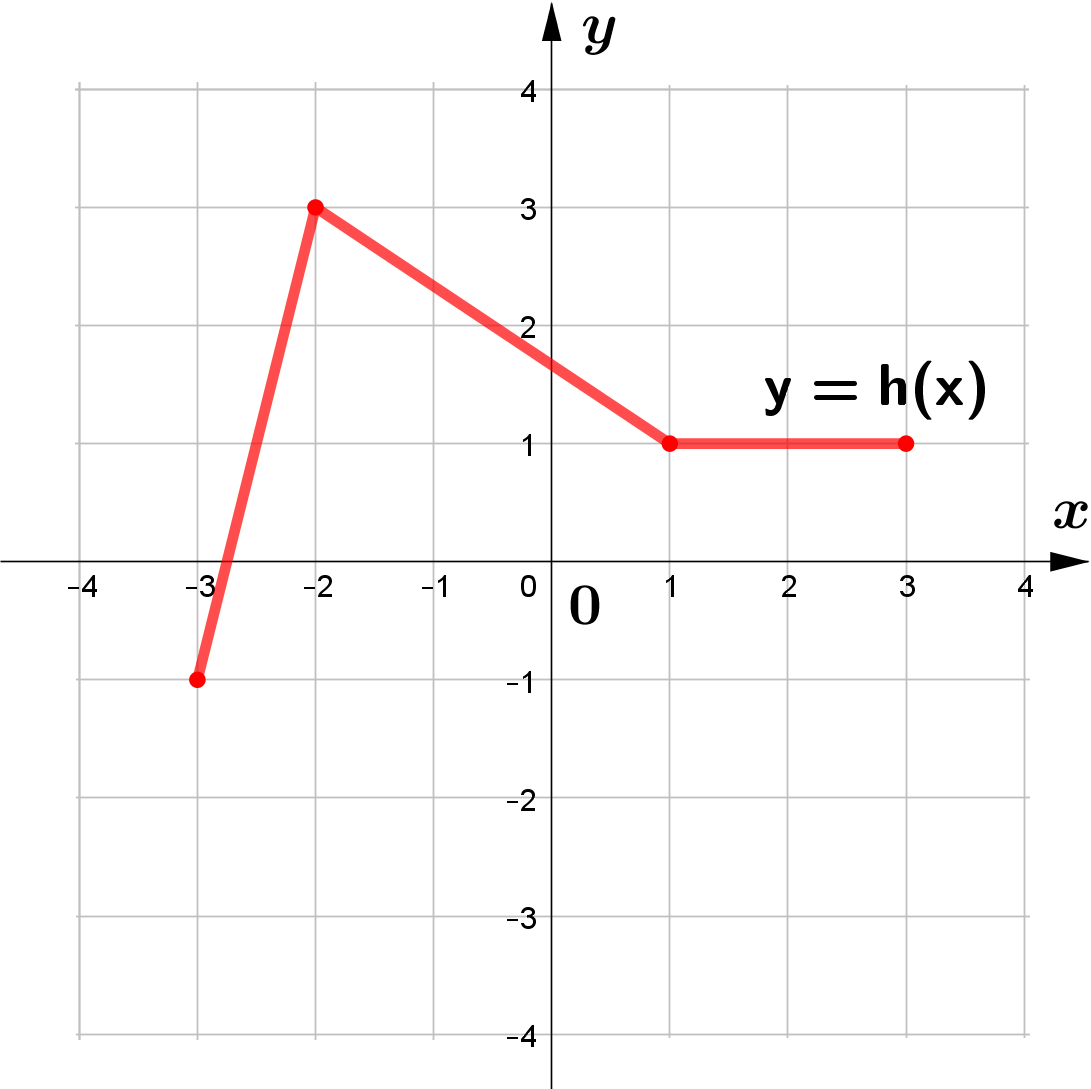
Sketch the graphs of each of the following functions.

$\begin{array}{l}
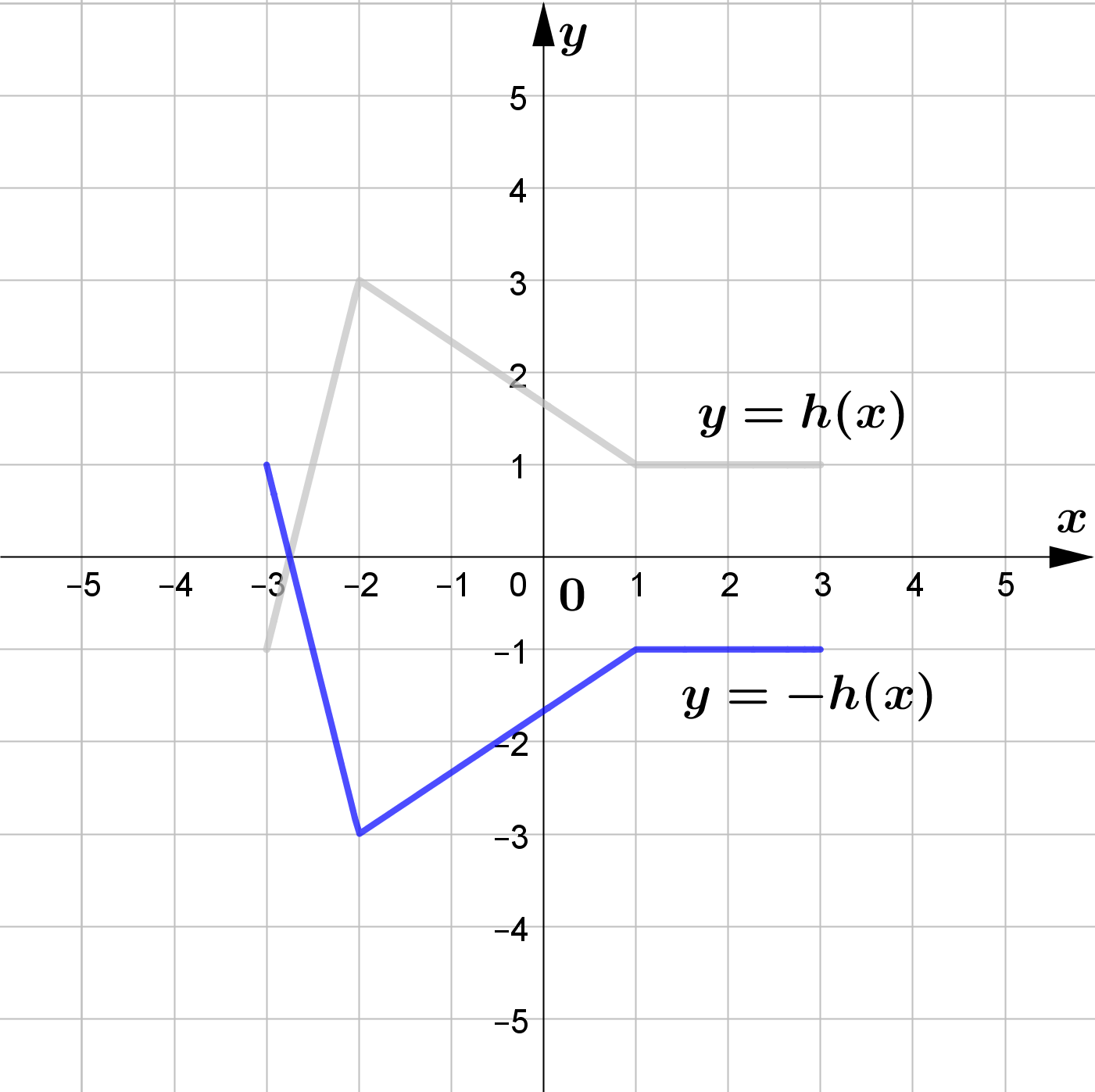
\text{(a) } y=-h(x)\\\\
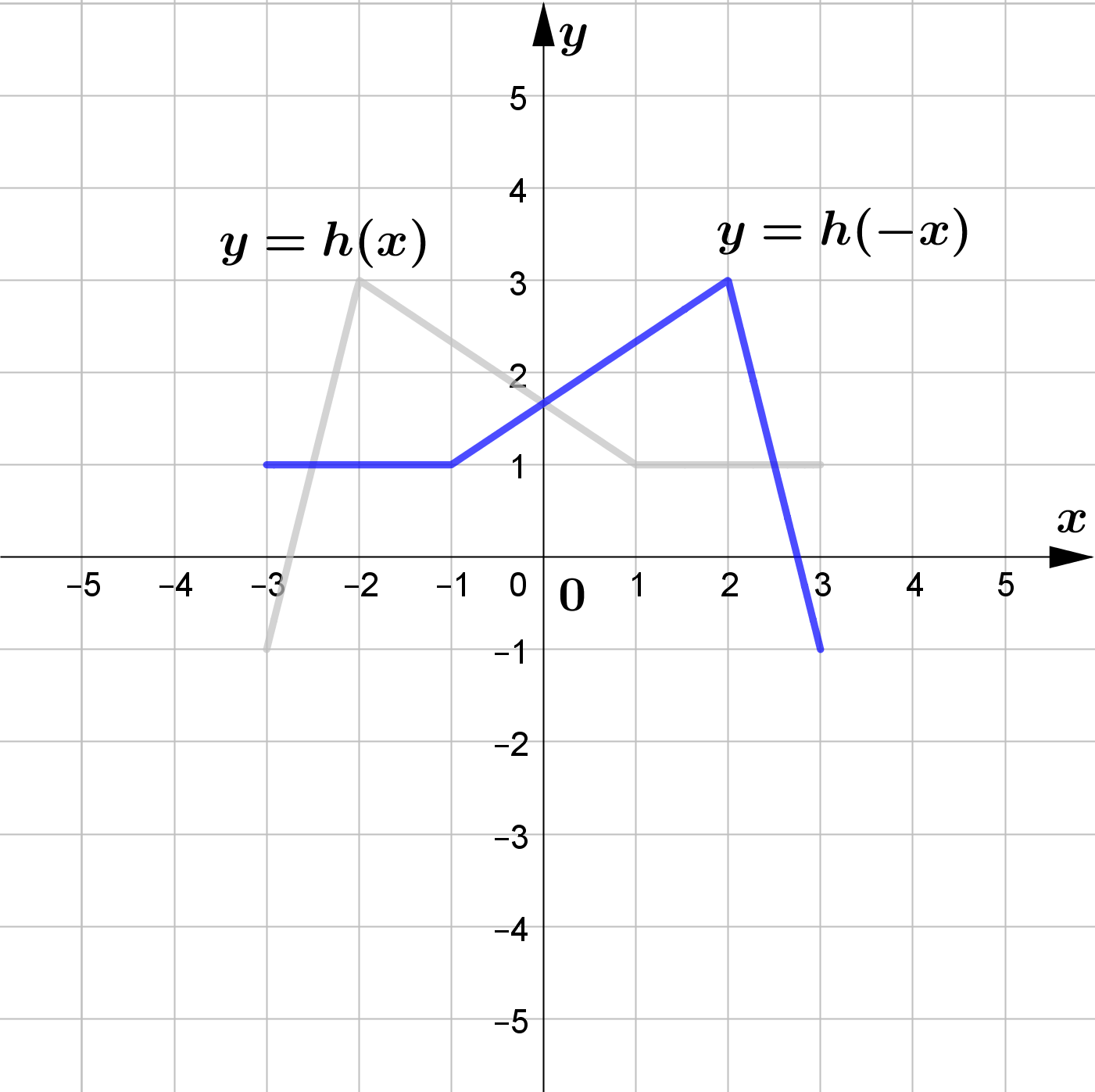
\text{(b) } y=h(-x)\\\\
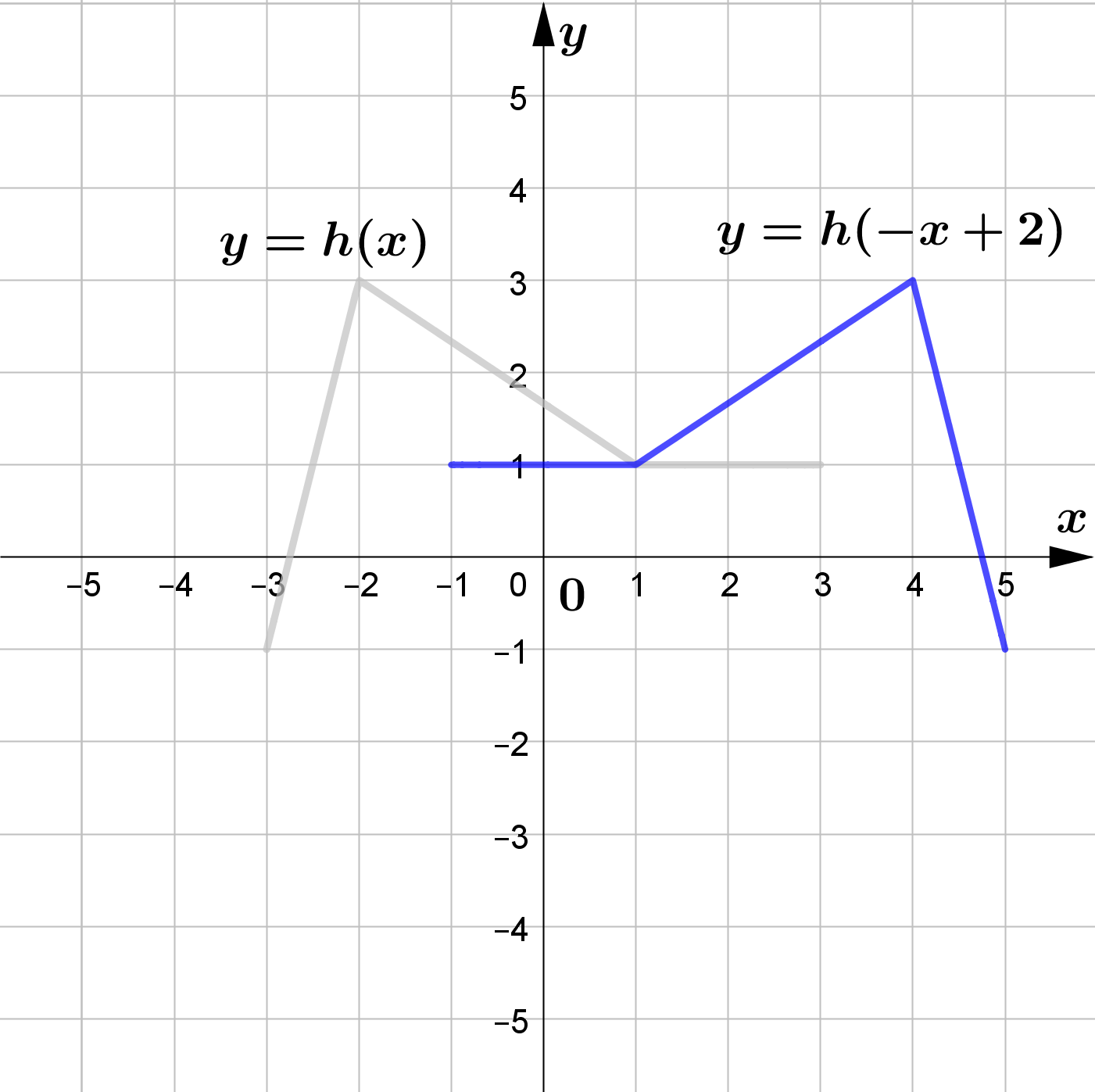
\text{(c) } y=h(-x)+2\\\\
\text{(d) } h(x-2)
\end{array}$

SOLUTION
(a) $y=-h(x)$

(b) $y=y=h(-x)$

(d) $y=h(x-2)$

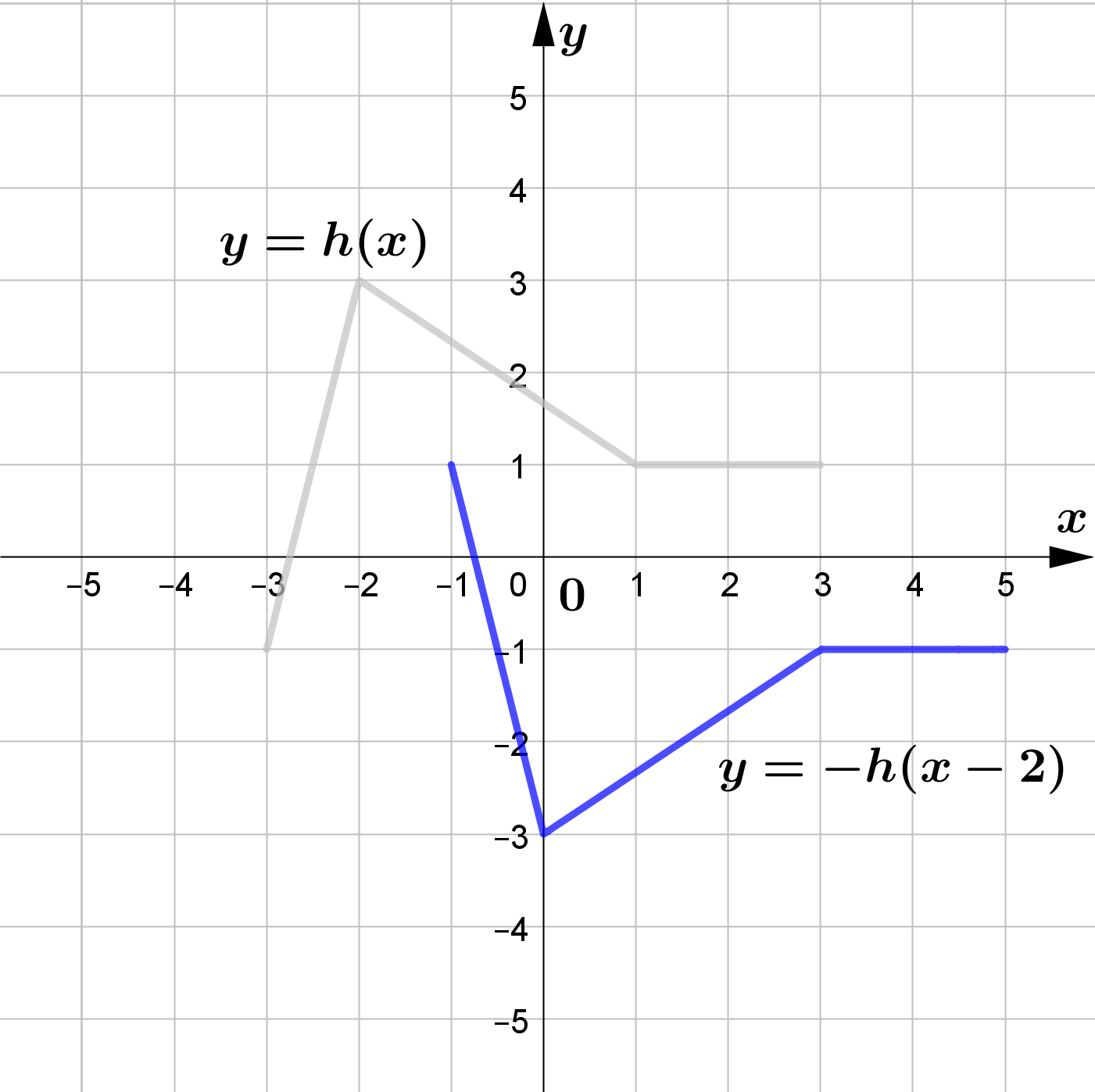
Question (4)

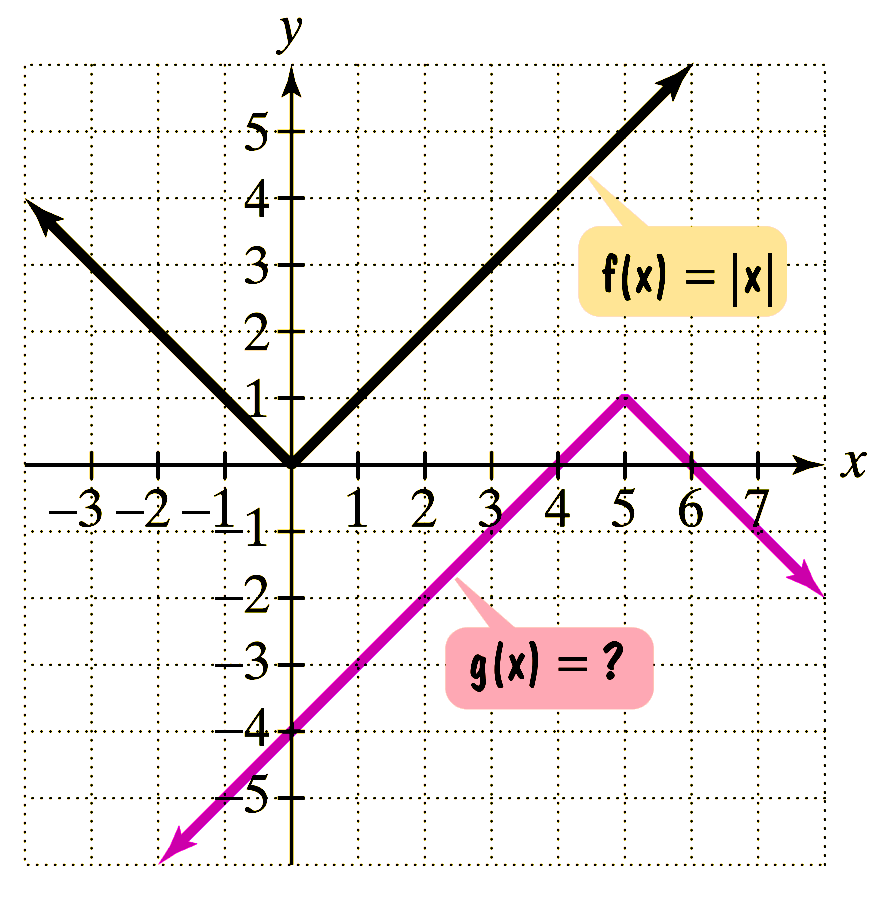
If $g$ is obtained from $f$ through a sequence of transformations, find an equation for $g$.

(a)

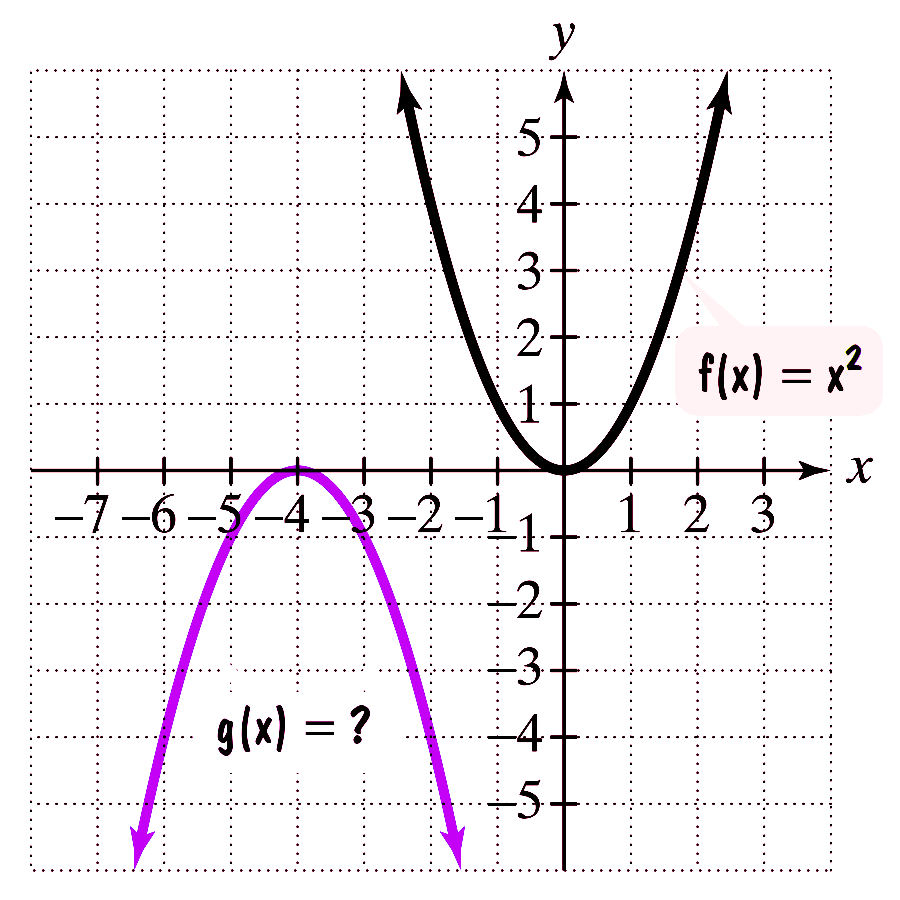
(b)

SOLUTION $\text{(a)}$

The graph of $g$ is obtained by shifting the graph of $f$, 4 units left and then reflecting in $x$-axis.

$g(x) = -f(x+4)$

$\text{(b)}$

The graph of $g$ is obtained by shifting the graph of $f$, 5 units left and 1 uint up and then reflecting in $x$-axis.

$g(x) = -f(x-5)+1$

Question (5)

Which of the following is true?

$\text{(a)}$	If $f(x)=\|x\|$ and $g(x)=\|x+3\|+3$, then the graph of $g$ is a translation of three units to the right and three units upward of the graph of $f$.
$\text{(b)}$	If $f(x)=-\sqrt{x}$ and $g(x)=\sqrt{-x}$, then $f$ and $g$ have identical graphs.
$\text{(c)}$	If $f(x)=x^{2}$ and $g(x)=-\left(x^{2}-2\right)$, then the graph of $g$ can be obtained from the graph of $f$ by a downward shift of two units and then reflecting in the $x$-axis.
$\text{(d)}$	If $f(x)=x^{3}$ and $g(x)=-(x-3)^{3}-4$, then the graph of $g$ can be obtained from the graph of $f$ by moving $f$ three units to the right, reflecting in the $x$-axis, and then moving the resulting graph down four units.

SOLUTION
$\begin{array}{l}
\text{(a) false}\\\\
\text{(b) false}\\\\
\text{(c) true}\\\\
\text{(d) true}
\end{array}$

Mathematics Spot