May-June-21-CIE-9709-21 : AS and A Level - Problems and Solutions
2021 (May-June) CIE (9709-Pure Mathematics 1), Paper 1/21 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။
Solve the inequality $|3x − 7| < |4x + 5|$.
[4]
By first expanding $\sin(\theta + 30^{\circ})$, solve the equation
$\sin(\theta + 30^{\circ})\operatorname{cosec}\theta = 2$
for $0^{\circ} < \theta < 360^{\circ}$.
[6]
(a) Show that $(\sec x+\cos x)^{2}$ can be expressed as $\sec ^{2} x+a+b \cos 2 x$,
where $a$ and $b$ are constants to be determined.
[2]
(b) Hence find the exact value of $\displaystyle\int_{0}^{\frac{1}{4} \pi}(\sec x+\cos x)^{2} dx$.
[4]
SOLUTION
A curve has parametric equations
$$x=\ln (2 t+6)-\ln t, \quad y=t \ln t .$$
(a) Find the value of $t$ at the point $P$ on the curve for which $x=\ln 4$.
[3]
(b) Find the exact gradient of the curve at $P$.
[5]
SOLUTION
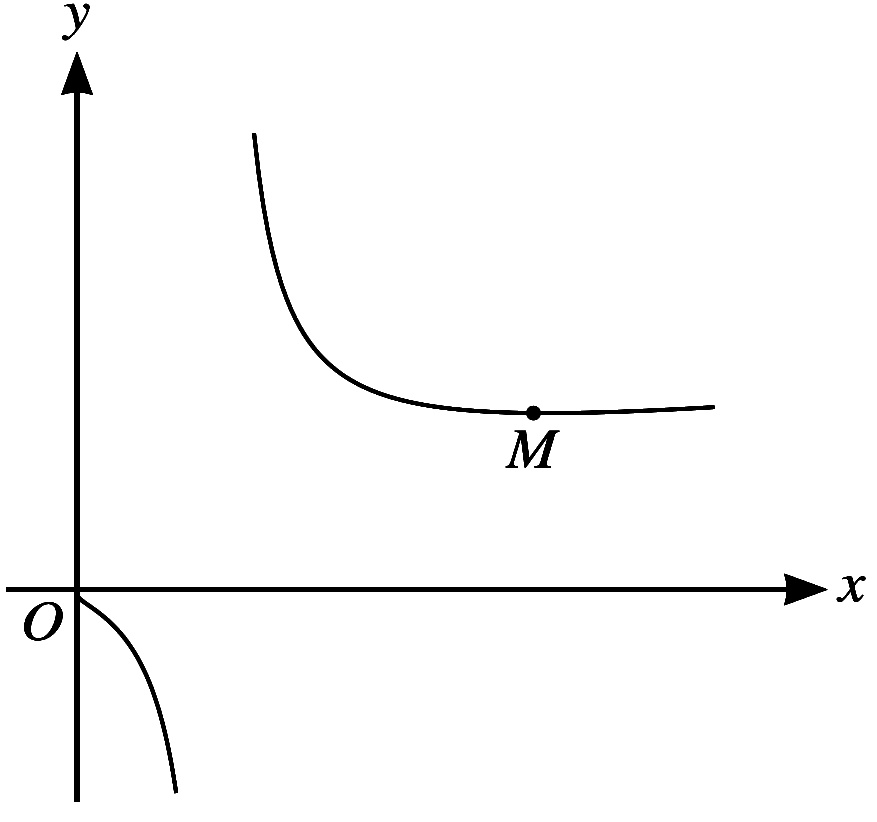
The diagram shows the curve with equation $y=\dfrac{3 x+2}{\ln x}$. The curve has a minimum point $M$.
(a) Find an expression for $\dfrac{dy}{dx}$ and
show that the $x$-coordinate of $M$ satisfies the equation $x=\dfrac{3 x+2}{3 \ln x}$.
[3]
(b) Use the equation in part (a) to show by calculation that the $x$-coordinate of $M$ lies between
$3$ and $4$.
[2]
(c) Use an iterative formula, based on the equation in part (a), to find the $x$-coordinate of $M$ correct
to $5$ significant figures. Give the result of each iteration to $7$ significant figures.
[3]
(a) Use the trapezium rule with three intervals to find an approximation to
$\displaystyle\int_{1}^{4} \frac{6}{1+\sqrt{x}}dx$.
Give your answer correct to $5$ significant figures.
[3]
(b) Find the exact value of $\displaystyle\int_{1}^{4} 2 e^{\frac{1}{2} x-2}dx$.
[3]
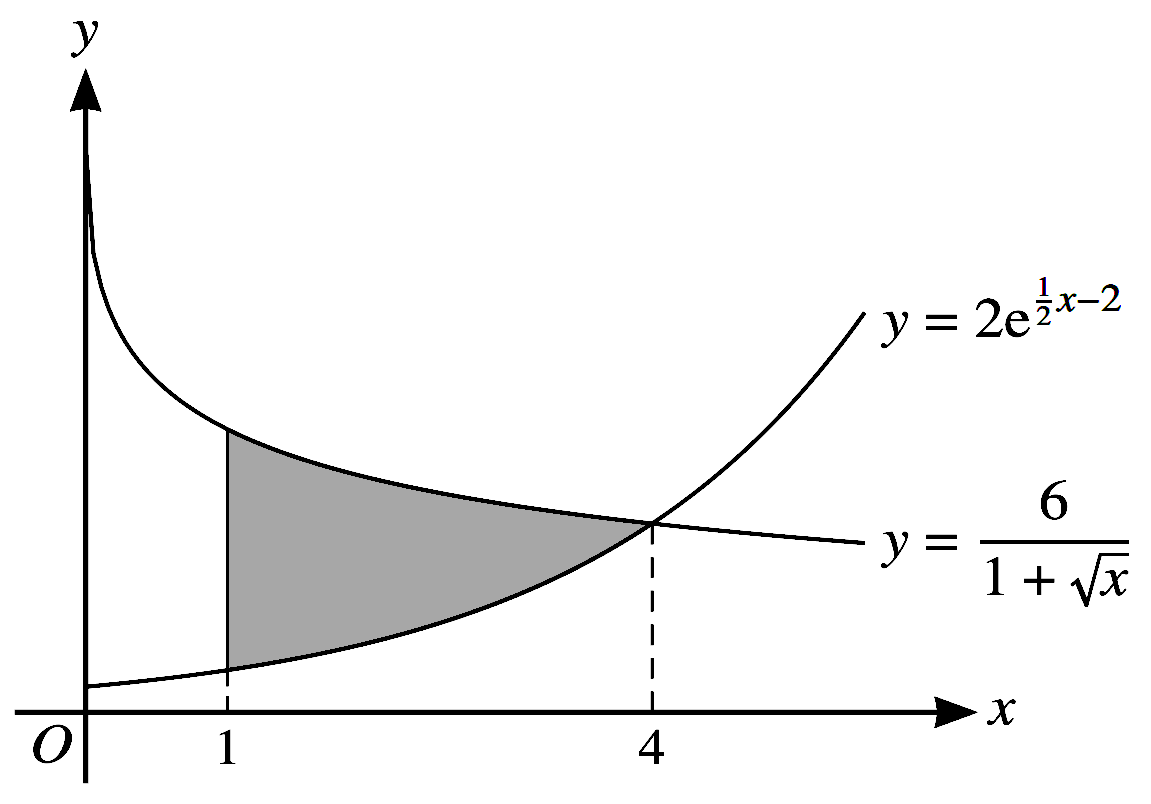
(c) The diagram shows the curves $y=\dfrac{6}{1+\sqrt{x}}$ and $y=2 e^{\frac{1}{2} x-2}$ which meet
at a point with $x$-coordinate $4$ . The shaded region is bounded by the two curves and the line $x=1$.
Use your answers to parts (a) and (b) to find an approximation to the area of the shaded region.
Give your answer correct to $3$ significant figures.
[2]
(d) State, with a reason, whether your answer to part (c) is an over-estimate or under-estimate of the
exact area of the shaded region.
[1]
SOLUTION
The polynomial $\mathrm{p}(x)$ is defined by
$p(x)=a x^{3}-11 x^{2}-19 x-a,$
where $a$ is a constant. It is given that $(x-3)$ is a factor of $p(x)$.
(a) Find the value of $a$.
[2]
(b) When $a$ has this value, factorise $p(x)$ completely.
[3]
(c) Hence find the exact values of $y$ that satisfy the equation
$p\left(e^{y}+e^{-y}\right)=0$.
[4]
SOLUTION
$\begin{aligned}
&|3 x-7|< |4 x+5|\\\\
&\sqrt{(3 x-7)^{2}}< \sqrt{(4 x+5)^{2}}\\\\
&(3 x-7)^{2}< (4 x+5)^{2}\\\\
&(3 x-7)^{2}-(4 x+5)^{2}< 0\\\\
&(3 x-7-4 x-5)(3 x-7+4 x+5)< 0\\\\
&(-x-12)(7 x-2)< 0\\\\
&-(x+12)(7 x-2)< 0\\\\
&(x+12)(7 x-2)>0\\\\
&x< -12 \text { or } x>\frac{2}{7}
\end{aligned}$
SOLUTION
$\begin{aligned}
&\sin \left(\theta+30^{\circ}\right)=\sin \theta \cos 30^{\circ}+\cos \theta \sin 30^{\circ}\\\\
&\sin (\theta+30^{\circ}) \operatorname{cosec} \theta=2\\\\
&\left(\sin \theta \cos 30^{\circ}+\cos \theta \sin 30^{\circ}\right) \frac{1}{\sin \theta}=2\\\\
&\cos 30^{\circ}+\cot \theta \sin 30^{\circ}=2\\\\
&\frac{\sqrt{3}}{2}+\frac{1}{2} \cot \theta=2\\\\
&\cot \theta=4-\sqrt{3}\\\\
&\tan \theta=\frac{1}{4-\sqrt{3}}\\\\
\therefore\ &\theta=23.8^{\circ}\ \text{ or }\ \theta=203.8^{\circ}
\end{aligned}$
$\begin{aligned}
\text{ (a) } \quad & (\sec x+\cos x)^{2} \\\\
=&\ \sec ^{2} x+2 \sec x \cos x+\cos ^{2} x \\\\
=&\ \sec ^{2} x+\frac{2}{\cos x} \cdot \cos x+\cos ^{2} x \\\\
=&\ \sec ^{2} x+2+\cos ^{2} x \\\\
=&\ \frac{1}{2}\left(2 \sec ^{2} x+4+2 \cos ^{2} x-1+1\right) \\\\
=&\ \frac{1}{2}\left(2 \sec ^{2} x+5+\cos 2 x\right) \\\\
=&\ \sec ^{2} x+\frac{5}{2}+\frac{1}{2} \cos 2 x\\\\
\text{ (b) } \quad & \int_{0}^{\frac{\pi}{4}}(\sec x+\cos x)^{2} d x \\\\
=&\ \int_{0}^{\frac{\pi}{4}}\left(\sec ^{2} x+\frac{5}{2}+\frac{1}{2} \cos x x\right) d x \\\\
=&\ {\left[\tan x+\frac{5}{2} x+\frac{1}{4} \sin 2 x\right]_{0}^{\frac{\pi}{4}} } \\\\
=&\ 1+\frac{5 \pi}{8}+\frac{1}{4} \\\\
=&\ \frac{5}{8}(2+5 \pi)
\end{aligned}$
$\begin{aligned}
\text{ (a) } \quad\quad x &=\ln (2 t+6)-\ln t \\\\
y &=t \ln t \\\\
\text { When } x &=\ln 4 \\\\
\ln 4 &=\ln (2 t+6)-\ln t \\\\
\ln 4 &=\ln \left(\frac{2 t+6}{t}\right) \\\\
\therefore \frac{2 t+6}{t} &=4 \\\\
\therefore 2 t+6 &=4 t \\\\
2 t &=6 \\\\
t &=3\\\\
\frac{d x}{d t} &=\frac{2}{2 t+6}-\frac{1}{t} \\\\
&=-\frac{6}{t(2 t+6)} \\\\
\frac{d y}{d t} &=1+\ln t \\\\
\frac{d y}{d x} &=\frac{d y / d t}{d x / d t} \\\\
&=-\frac{t(2 t+6)(1+\ln t)}{6}\\\\
\end{aligned}$
$\text{ (b) } \ $ At the point $P$,
$\begin{aligned}
&\\
\qquad\frac{d y}{d x} &=-\frac{3(12)(1+\ln 3)}{6} \\\\
&=-6(1+\ln 3)\\\\
\end{aligned}$
$\quad\therefore\ $ The gradient of the curve at the point $P$ is $-6(1+\ln 3).$
SOLUTION
$\begin{aligned}
\text{ (a) } \quad & y=\dfrac{3 x+2}{\ln x} \\\\
& \dfrac{d y}{d x}=\dfrac{3 \ln x-\dfrac{3 x+2}{x}}{\ln ^{2} x} \\\\
& \dfrac{d y}{d x}=0, \text { Shen } \\\\
& \dfrac{3 \ln x-\dfrac{3 x+2}{x}}{\ln ^{2} x}=0 \\\\
\therefore\ & 3 \ln x-\dfrac{3 x+2}{x}=0 \quad \left(\because \ln ^{2} x \neq 0\right) \\\\
\therefore\ & 3 \ln x=\dfrac{3 x+2}{x}\\\\
\therefore\ x &=\dfrac{3 x+2}{3 \ln x} \\\\
\end{aligned}$
$\begin{aligned}
\text{ (b) } \quad x-\dfrac{3 x+2}{3 \ln x} &=0 \quad (\text {by part (a)}) \\\\
\text { Let } f(x) &=x-\dfrac{3 x+2}{3 \ln x} \\\\
f(3) &=3-\dfrac{11}{3 \ln 3} \\\\
&=-0.34 \\\\
f(4) &=4-\dfrac{14}{3 \ln 4} \\\\
&=0.63\\\\
\end{aligned}$
Since $f(3)$ and $f(4)$ has opposite signs, there is one root for $f(x)=0$ between $x=3$ and $x=4.\\\\ $
$\therefore$ The $x$-coordinates of $m$ lies between $x=3$ and $x=4.\\\\ $
As we have $x=\dfrac{3 x+2}{3 \ln x},\\\\ $
$\text{let } x_{n+1}=\dfrac{3 x_{n}+2}{3 \ln x_{n}}.\\\\ $
$\begin{array}{|c|c|c|}
\hline n & x_{n} & x_{n+1}=\dfrac{3 x+2}{3 \ln x} \\
\hline 1 & 3.5 & 3.325982 \\
\hline 2 & 3.325982 & 3.322321 \\
\hline 3 & 3.322321 & 3.322319 \\
\hline 4 & 3.322319 & 3.322319 \\
\hline
\end{array}$
$\therefore\ $ The $x$ coordinate of $M=3.3223$ (correct to 5 sigmiticant figures)
Let $y=\dfrac{6}{1+\sqrt{x}}\\\\ $
For $\displaystyle\int_{1}^{4} y d x$,
$\begin{aligned}
&\\
a &=1, b=4, n=3 \text { (given) } \\\\
\therefore \quad h &=\frac{b-a}{n} \\\\
&=\frac{4-1}{3} \\\\
&=1\\\\
\end{aligned}$
$\begin{array}{|c||c|c|c|c|}
\hline \quad x\quad & \quad 1\quad & \quad 2\quad & \quad 3\quad & \quad 4\quad \\
\hline \quad y\quad & \quad 3 \quad & \quad 2.4853\quad & \quad 2.1962\quad & \quad 2\quad \\
\hline
\end{array}$
$\begin{aligned}
& \displaystyle\int_{1}^{4} \frac{6}{1+\sqrt{x}} d x \\\\
=&\ \frac{1}{2}[(3+2)+2(2.4853+2.1962)] \\\\
=&\ 7.1815
\end{aligned}$
$\begin{aligned}
\text{(b)}\quad & \int_{1}^{4} 2 e^{\frac{1}{2} x-2} d x \\\\
=&\ 2 \int_{1}^{4} e^{\frac{1}{2} x-2} 2 \cdot d\left(\frac{1}{2} x-2\right) \\\\
=&\ 4 \int_{1}^{4} e^{\frac{1}{2} x-2} d\left(\frac{1}{2} x+2\right) \\\\
=&\ 4\left[e^{\frac{1}{2} x-2}\right]^{4} \\\\
=&\ 4\left[e^{0}-e^{-3 / 2}\right] \\\\
=&\ 4\left[1-e^{-3 / 2}\right]\\\\
\end{aligned}$
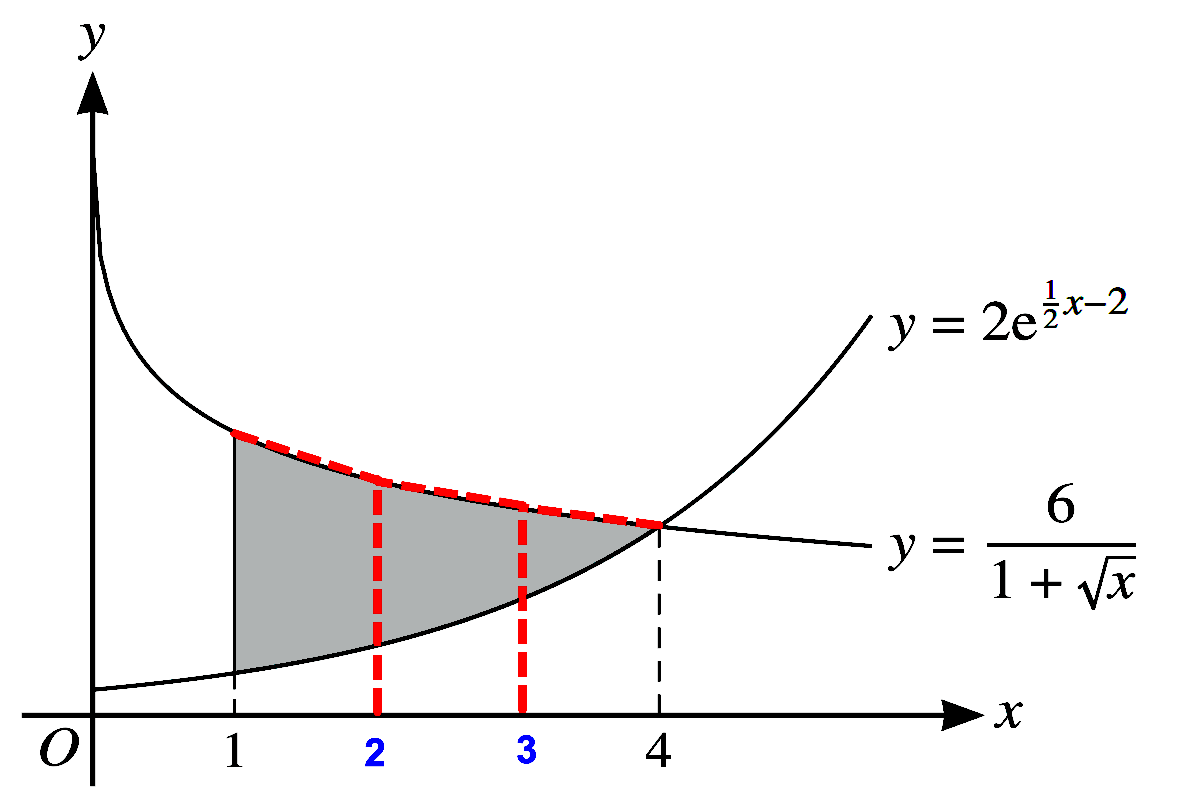
$\text{(c)}\quad$ Let $y_{1}=\frac{6}{1+\sqrt{x}}$ and $y_{2}=2 e^{\frac{1}{2} x-2}\\\\ $.
For a given interval,
Let the area under $y_{1}$ be $A_{1}$ and that under $y_{2}$ be $A_{2}\\\\ $.
By part (a), $A_{1}=7.1815\\\\ $
By part (b), $A_{2}=4\left[1-e^{-3 / 2}\right]\\\\ $
The approximate area of shaded region
$\begin{aligned}
&\\
&=A_{1}-A_{2} \\\\
&=7.1815-4\left[1-e^{-3 / 2}\right] \\\\
&=4.07\\\\
\end{aligned}$
$\text{(d)}\quad$ It can be seen from the diagram that the approximate area of the shade region is
an over-estimate since the top edges of the strips of $A_1$ all lie above the curve.
SOLUTION
$\begin{aligned}
& p(x)=a x^{3}-11 x^{2}-19 x-a \\\\
&(x-3) \text { is a factor of } p(x) \\\\
\therefore\ & p(3)=0 \\\\
& 27 a-99-57-a=0 \\\\
& 26 a=156 \\\\
& a=6 \\\\
\therefore\quad & p(x)=6 x^{3}-11 x^{2}-19 x-6\\\\
&\text{Let } 6 x^{3}-11 x^{2}-19 x-6=(x-3)\left(6 x^{2}+k x+2\right)\\\\
\therefore \quad & k-18 =-11 \\\\
\therefore\quad &k =7 \\\\
\therefore \quad &p(x) =(x-3)\left(6 x^{2}+7 x+2\right) \\\\
\therefore \quad & p(x)=(x-3)(3 x+2)(2 x+1)\\\\
&p\left(e^{y}+e^{-y}\right)=0 \\\\
&\left(e^{y}+e^{-y}-3\right)\left(3\left(e^{y}+e^{-y}\right)+2\right)\left(2\left(e^{y}+e^{-y}\right)+1\right)=0 \\\\
&e^{y}+e^{-y}=3 \text { or } e^{y}+e^{-y}=-\frac{2}{3} \text { or } e^{y}+e^{-y}=-\frac{1}{2} \\\\
&\text {Since } e^{y}+e^{-y}>0, \\\\
&e^{y}+e^{-y}=3 \text { is only a unique solution. } \\\\
&e^{2 y}+1=3 e^{y} \\\\
&\left(e^{y}\right)^{2}-3 e^{y}+1=0\\\\
&\left(e^{y}\right)^{2}-3 e^{y}+\frac{9}{4}=\frac{5}{4} \\\\
&\left(e^{y}-\frac{3}{2}\right)^{2}=\frac{5}{4} \\\\
\therefore \quad & e^{y}=\frac{3 \pm \sqrt{5}}{2} \\\\
\therefore \quad & y=\ln \frac{3+\sqrt{5}}{2} \text { or } y=\ln \frac{3-\sqrt{5}}{2}
\end{aligned}$

Post a Comment for "May-June-21-CIE-9709-21 : AS and A Level - Problems and Solutions"