Analytic Geometry : The Circles
Circle တစ်ခု၏ ဗဟို၊ အချင်းဝက်ကို သိလျှင် Circle Equation ကို ရှာယူနိုင်ကြောင်း Conic Sections တွင် တင်ပြခဲ့ပြီး ဖြစ်ပါသည်။ ယခုသင်ခန်းစာတွင် circle တစ်ခု၏ ဂုဏ်သတ္တိများကို အသုံးပြု၍ analytic geometry ဆိုင်ရာ IGCSE A Level ပုစ္ဆာများနှင့် အဖြေများကို တင်ပြထားပါသည်။
-
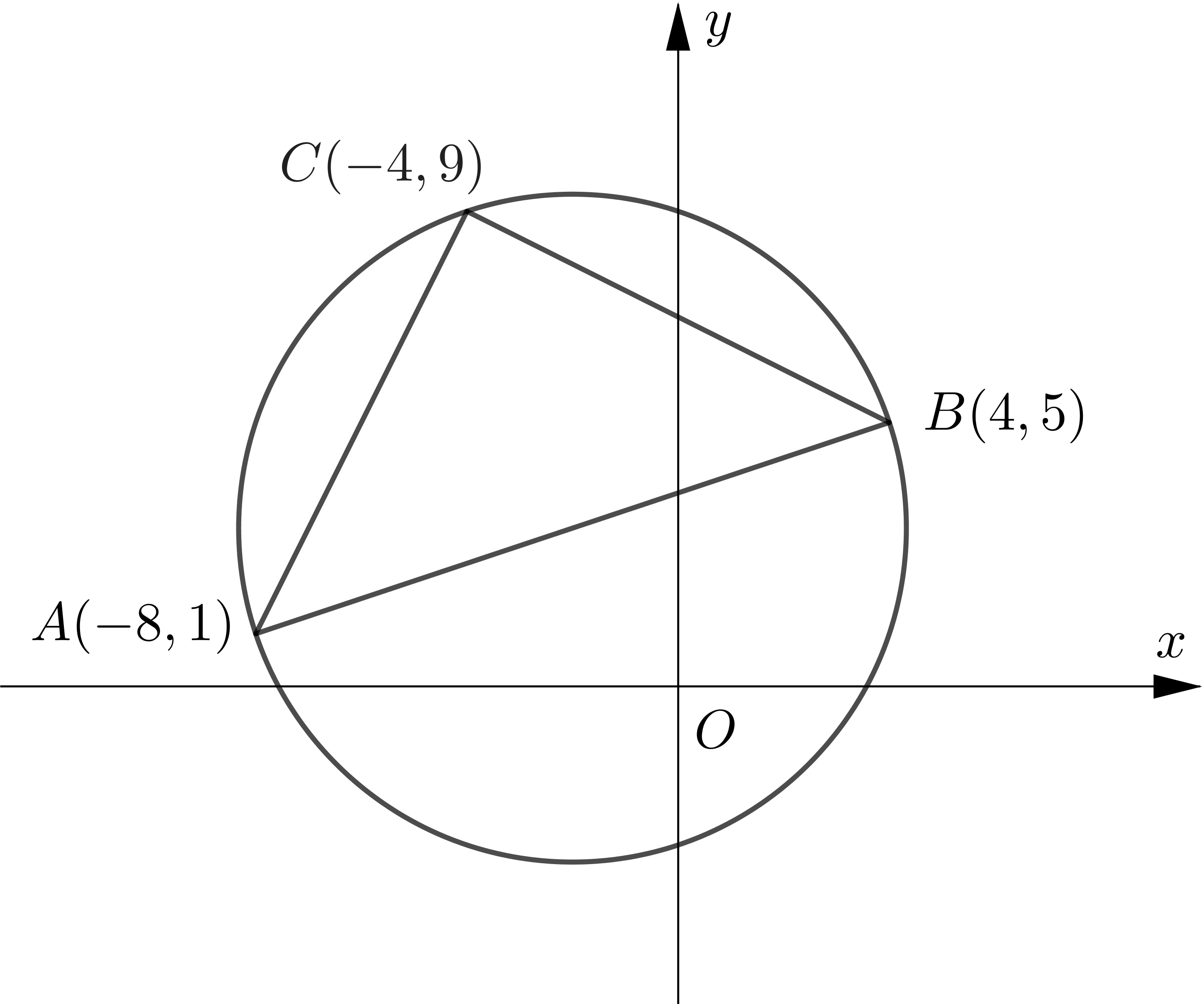
The points $A(-8,1), B(4,5)$ and $C(-4,9)$ lie on the circle, as shown in the diagram.
(a) Show that $A B$ is a diameter of the circle.
(b) Find an equation of the circle.
SOLUTION
$\begin{aligned}
&A:\ (-8,1) \\\\
&B:\ (4,5) \\\\
&C:\ (-4,9) \\\\
\end{aligned}$
$\begin{aligned}
\text { gradient of } A C &=\dfrac{9-1}{-4+8} \\\\
&=2\\\\
\text { gradient of } B C &=\dfrac{9-5}{-4-4} \\\\
&=-\dfrac{1}{2}\\\\
\therefore\ \text { gradient of } & A C \times \text { gradient of } B C\\\\
&=2 \times\left(-\dfrac{1}{2}\right)\\\\
&=-1 \\\\
\end{aligned}$
$\therefore A C \perp B C\\\\ $
$\therefore\ A B \text { is a diameter. }\\\\ $
Let $P$ be the midpoint of $A B.\\\\ $
$\therefore P $ is the centre of circle.
$\begin{aligned}
&\\
P &=\left(\dfrac{-8+4}{2}, \dfrac{1+5}{2}\right)=(-2,3) \\\\
\therefore\ P C &=\sqrt{(-2+4)^{2}+(3-9)^{2}} \\\\
&=\sqrt{4+36} \\\\
&=\sqrt{40}\\\\
\end{aligned}$
Thus, the equation of the circle is
$\begin{aligned}
&\\
(x+2)^{2}+(y-3)^{2}&=40
\end{aligned}$
-
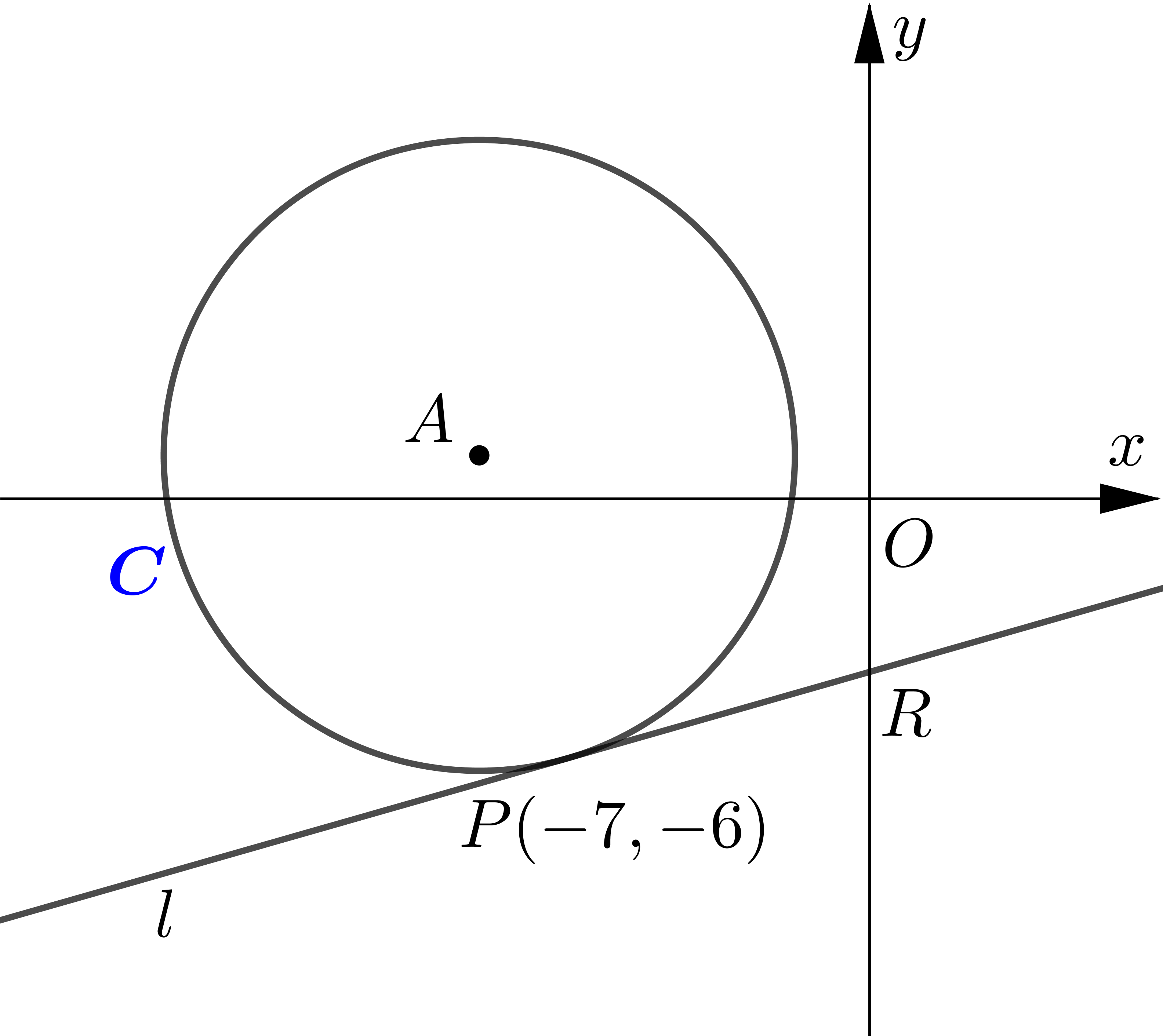
The circle $C$ has equation $x^{2}+18 x+y^{2}-2 y+29=0$.
(a) Verify the point $P(-7,-6)$ lies on $C$.
(b) Find an equation for the tangent to $C$ at the point $P$, giving your answer in the form $y=m x+b$.
(c) Find the coordinates of $R$, the point of intersection of the tangent and
(d)Find the area of the triangle $A P R$.
SOLUTION

$C: x^{2}+18 x+y^{2}-2 y+29=0\\\\ $
When $x=-7, y=-6\\\\ $
$\begin{aligned}
&(-7)^{2}+18(-7)+(-6)^{2}-2(-6)+29\\\\
=&\ 49-126+36+12+29\\\\
=&\ 0\\\\
\end{aligned}$
$\therefore(-7,-6)$ lies on $C .\\\\ $
$C: x^{2}+18 x+y^{2}-2 y+29=0\\\\ $
$x^{2}+18 x+81+y^{2}-2 y+1=-29+81+1\\\\ $
$(x+9)^{2}+(y-1)^{2}=53\\\\ $
$\therefore$ centre $(A):(-9,1)\\\\ $
$\begin{aligned}
\text{gradent of } A P &=\dfrac{1+6}{-9+7} \\\\
&=-\dfrac{7}{2} \\\\
\text{gradient of tangent at } P&=\dfrac{2}{7}\\\\
\end{aligned}$
$\therefore$ Equation of tangent at $P$ is
$\begin{aligned}
&\\
y+6 &=\dfrac{2}{7}(x+7) \\\\
\therefore y&=\dfrac{2}{7} x-4\\\\
\end{aligned}$
When the tangent cuts $y$ axis, $x=0\\\\ $.
$\begin{aligned}
\therefore\ y &=\dfrac{2}{7}(0)-4=-4 \\\\
\therefore\ R: &(0,-4) \\\\
A P &=\text { length of radius } \\\\
&=\sqrt{53} \\\\
P R &=\sqrt{(0+7)^{2}+(-4+6)^{2}} \\\\
&=\sqrt{53}\\\\
&\text{area of } \triangle A P R\\\\
&=\dfrac{1}{2} \times A P \times P R \\\\
&=\dfrac{1}{2} \times \sqrt{53} \times \sqrt{53} \\\\
&=\dfrac{53}{2}
\end{aligned}$
-
The tangent to the circle $(x+4)^{2}+(y-1)^{2}=242$ at $(7,-10)$ meets the $y$-axis at $S$ and the $x$-axis at $T$.
(a) Find the coordinates of $S$ and $T$.
(b) Hence, find the area of $\triangle O S T$, where $O$ is the origin.
SOLUTION

Circle: $(x+4)^{2}+(y-1)^{2}=2 y 2\\\\ $
Centre: $(-4,1)\\\\ $
Tangent point: $(7,-10)\\\\ $
let $m_{1}$ be the gradient of
the line parsing through $(-4,1)$
and $(7,-10)\\\\ $.
$m_{1}=\dfrac{-10-1}{7+4}=-1\\\\ $
Let the gradient of toungent to circle at $(7,-10)$ be $m_{2}.\\\\ $
$\therefore m_{2}=-\dfrac{1}{m_{1}}=1 .\\\\ $
Let the coordinates of the point $S$ and $T$ be $(0, b)$ and $(a, 0)\\\\ $.
$\begin{aligned}
\therefore \dfrac{b-(-10)}{0-7} &=1 \\\\
b &=-17 \\\\
\dfrac{0-(-10)}{a-7} &=1 \\\\
a &=17 \\\\
S &=(0,-17) \\\\
T &=(17,0)\\\\
\text{area of }\triangle OST &=\dfrac{1}{2}|a||b| \\\\
&=\dfrac{1}{2}|17|-17 \mid \\\\
&=\dfrac{289}{2}
\end{aligned}$
-
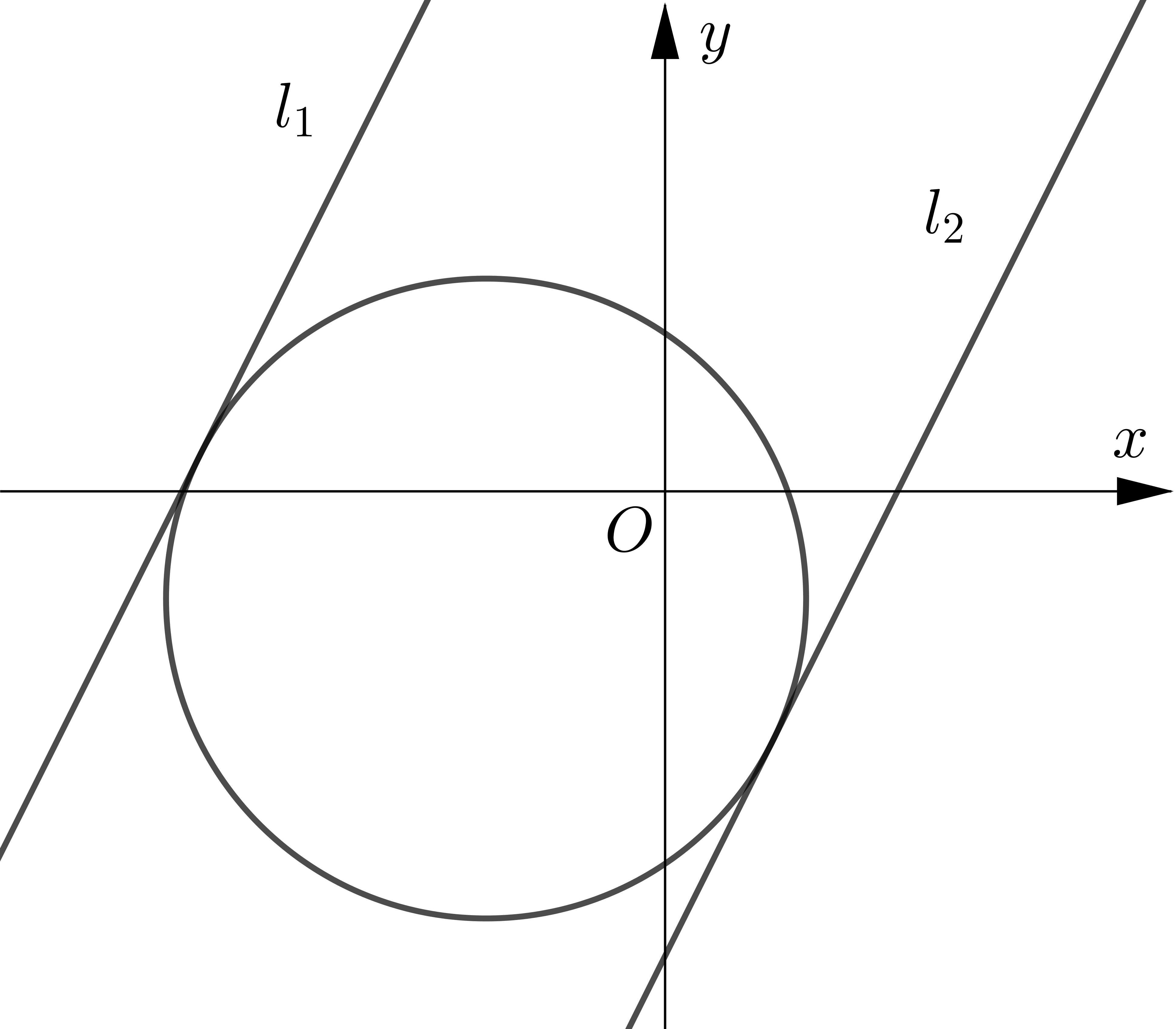
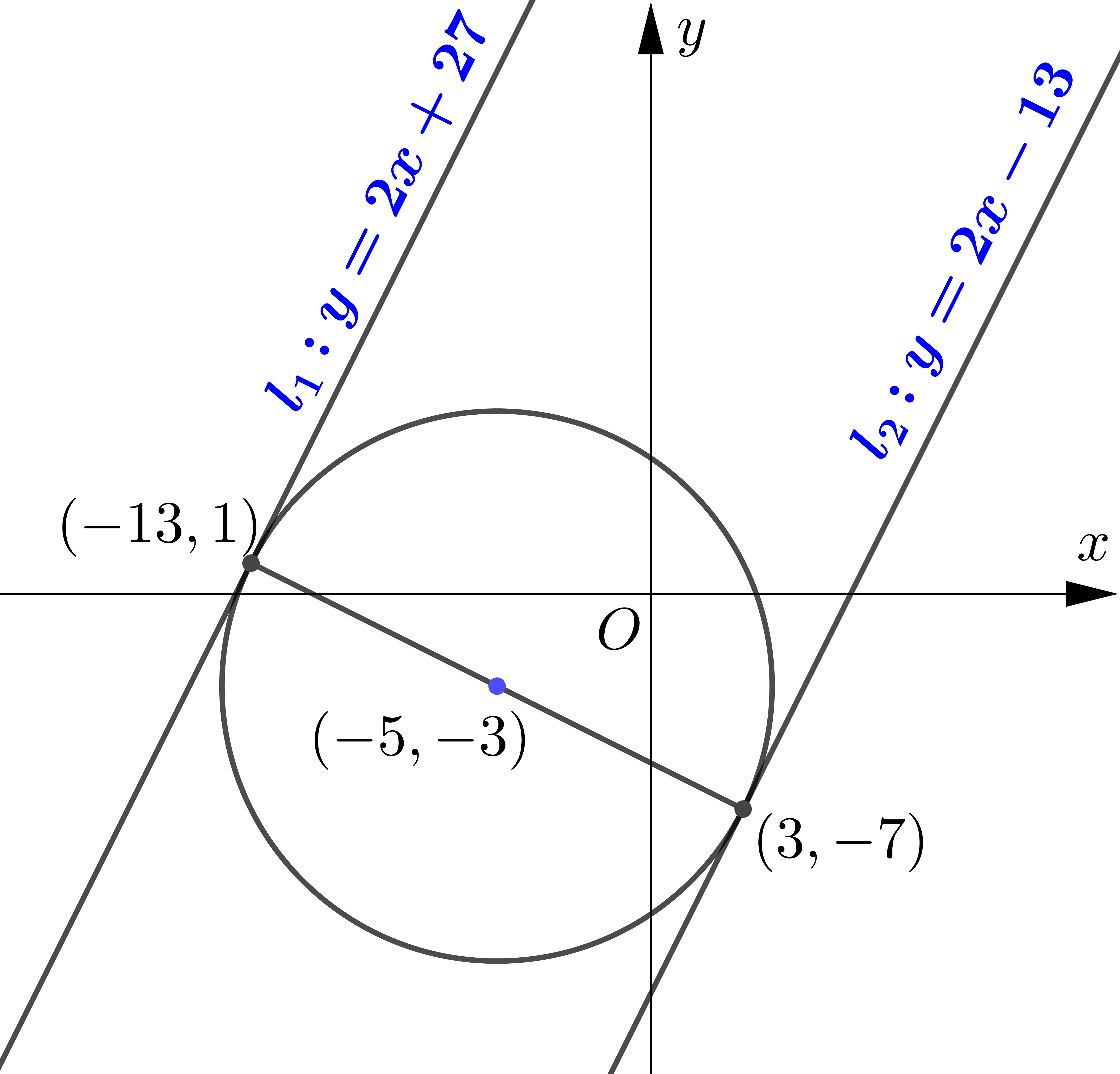
The circle $C$ has equation $(x+5)^{2}+(y+3)^{2}=80$.
The line $l$ is a tangent to the circle and has gradient $2 .$
Find two possible equations for $l$ giving your answers in the form $y=m x+c$.
SOLUTION
$C:(x+5)^{2}+(y+3)^{2}=80\\\\ $
Centre: $(-5,-3)\\\\ $
radius $=\sqrt{80}\\\\ $
Let the gradient of tangent be $m.\\\\ $
$\therefore m=2\\\\ $
Let the point where the tangent touches the circle be $(a, b).\\\\ $
$\begin{aligned}
\therefore\ \dfrac{b+3}{a+5} &=-\dfrac{1}{2} \\\\
2 b+6 &=-a-5 \\\\
a &=-2 b-11\\\\
\end{aligned}$
$(a, b)$ lies on circle.
$\begin{aligned}
&\\
\therefore(a+5)^{2}+(b+3)^{2}&=80 \\\\
(-2 b-11+5)^{2}+(b+3)^{2}&=80\\\\
\end{aligned}$
Solving equation, $b=-7$ or $b=1\\\\ $
$\begin{aligned}
b=-7 \Rightarrow & a=-2(-7)-11=3 \\\\
b=1 \Rightarrow & a=-2(1)-11=-13\\\\
\end{aligned}$
$\therefore$ At $(3,-7)$, the equation of tangent is
$\begin{aligned}
&\\
y+7 &=2(x-3) \\\\
y &=2 x-13\\\\
\end{aligned}$
At $(-13,1)$, the equation of tangent is
$\begin{aligned}
&\\
y-1&=2(x+13) \\\\
y&=2 x+27
\end{aligned}$
- The line with equation $2 x+y-5=0$ is a tangent to the circle with equation
$(x-3)^{2}+(y-p)^{2}=5$.
(a) Find the two possible values of $p$.
(b) Write down the coordinates of the centre of the circle in each case.
SOLUTION

Method 1
Line: $2 x+y-5=0\\\\ $
$y=5-2 x\\\\ $
$\therefore$ gradient of tangent $\left(m_{1}\right)=-2\\\\ $
Circle: $(x-3)^{2}+(y-p)^{2}=5\\\\ $
$\therefore$ centre: $(3, p)\\\\ $
radius $=\sqrt{5}\\\\ $
Let the point of tangency be $(a, 5-2 a).\\\\ $
$\therefore$ The gradient of the line passing through $(a, 5-2 a)$
and $(3, p)$ is $\dfrac{1}{2}.\\\\ $
$\begin{aligned}
\therefore \dfrac{5-2 a-p}{a-3} &=\dfrac{1}{2} \\\\
10-4 a-2 p &=a-3 \\\\
5 a &=13-2 p \\\\
a &=\dfrac{13-2 p}{5}\\\\
\end{aligned}$
$(a, 5-2 a)$ lies on circle.
$\begin{aligned}
&\\
\therefore(a-3)^{2}+(5-2 a-p)^{2} &=5 \\\\
\left(\dfrac{13-2 p}{5}-3\right)^{2}+\left(5+\dfrac{4 p-26}{5}-p\right)^{2} &=5 \\\\
\left(\dfrac{-2 p-2}{5}\right)^{2}+\left(\dfrac{-p-1}{5}\right)^{2} &=5 \\\\
\dfrac{4}{25}(p+1)^{2}+\dfrac{1}{25}(p+1)^{2} &=5\\\\
\end{aligned}$
$\begin{aligned}
\therefore(p+1)^{2} &=25 \\\\
p+1 &=\pm 5 \\\\
\therefore p &=-6 \text { or } p=4 \\\\
\text { Whan } p &=-6 \text {, centre }=(3,-6). \\\\
\text { When } p &=2 \text {, centre }=(3,4).\\\\
\end{aligned}$
Method 2
Line: $2 x+y-5=0\\\\ $
$y=5-2 x\\\\ $
Circle: $(x-3)^{2}+(y-p)^{2}=5\\\\ $
$\therefore$ Centre: $(3, p).\\\\ $
At the point of tangency,
$\begin{aligned}
&\\
(x-3)^{2}+(5-2 x-p)^{2}&=5\\\\
x^{2}-6 x+9+(5-2 x)^{2}-2 p(5-2 x)+p^{2}&=5 \\\\
x^{2}-6 x+9+25-20 x+4 x^{2}-10 p+4 p x+p^{2}-5&=0 \\\\
5 x^{2}+(4 p-26) x+\left(p^{2}-10 p+29\right)&=0\\\\
\end{aligned}$
Since the tangent touch the circle at only one point, the discriminant $=0. $
$\begin{aligned}
&\\
(4 p-26)^{2}-4 \times 5\left(p^{2}-10 p+29\right)&=0 \\\\
16 p^{2}-208 p+676-20 p^{2}+200 p-580&=0 \\\\
-4 p^{2}-8 p+96&=0 \\\\
p^{2}+2 p-24&=0 \\\\
(p+6)(p-4)&=0\\\\
\therefore p =-6 \text { or } p&=4 \\\\
\text { Whan } p =-6 \text {, centre }&=(3,-6). \\\\
\text { When } p =2 \text {, centre }&=(3,4).
\end{aligned}$
-
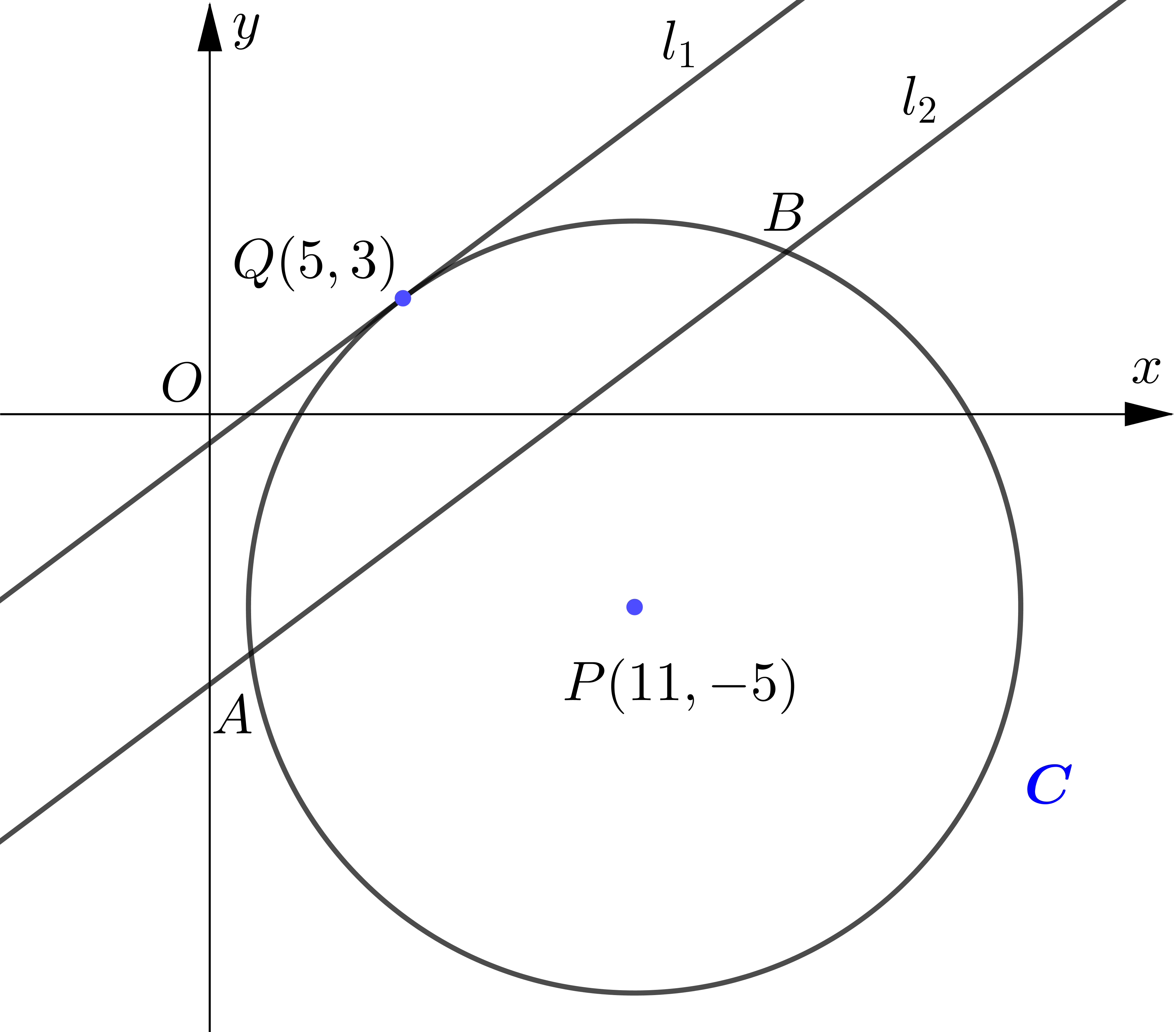
The circle $C$ has centre $P(11,-5)$ and passes through the point $Q(5,3)$.
(a) Find an equation for $C$.
The line $l_{1}$ is a tangent to $C$ at the point $Q$.
(b) Find an equation for $l_{1}$.
The line $l_{2}$ is parallel to $l_{1}$ and passes through the midpoint of $P Q .$
(c) Find the equation of $l_2$.
Given that $l_{2}$ intersects $C$ at $A$ and $B$. find the coordinates of points $A$ and $B$,
(d) find the length of the line segment $A B$, leaving your answer in its simplest surd form.
SOLUTION
Circle $C$ has centre at $P(11,-5)$ and passes through the point $Q(5,3)\\\\ $.
$\begin{aligned}
\therefore \text { radius } &=\sqrt{(11-5)^{2}+(-5-3)^{2}} \\\\
&=\sqrt{100} \\\\
&=10\\\\
\end{aligned}$
$\therefore$ Equation of $C$ is
$\begin{aligned}
&\\
(x-11)^{2}+(y+5)^{2}&=100\\\\
\end{aligned}$
$\begin{aligned}
\text { Gracient of } P Q &=\dfrac{3+5}{5-11} \\
&=-\dfrac{4}{3}\\\\
\end{aligned}$
$\therefore$ Gradient of tangent at $Q=\dfrac{3}{4}\\\\ $
Equation of tangent $l_{1}$ at $Q$ is
$\begin{aligned}
&\\
y-3 &=\dfrac{3}{4}(x-5) \\\\
4 y-12 &=3 x-15 \\\\
3 x-4 y &=3\\\\
\end{aligned}$
Midpoint of $PQ=\left(\dfrac{11+5}{2}, \dfrac{-5+3}{2}\right)=(8,-1)\\\\ $
The equation line $l_{2}$ prallel to $l_1$ and passing through $(8,-1)$ is
$\begin{aligned}
&\\
y+1&=\dfrac{3}{4}(x-8) \\\\
y&=\dfrac{3 x-28}{4}\\\\
\end{aligned}$
When $l_{2}$ intersects $C$.
$\begin{aligned}
&\\
&(x-11)^{2}+\left(\dfrac{3 x-28}{4}+5\right)^{2}=100 \\\\
&(x-11)^{2}+\left(\dfrac{3 x-8}{4}\right)^{2}=100 \\\\
&x^{2}-22 x+121+\dfrac{9 x^{2}-48 x+64}{16}=100 \\\\
&16 x^{2}-352 x+1936+9 x^{2}-48 x+64=1600 \\\\
&25 x^{2}-400 x+400=0 \\\\
&x^{2}-16 x+16=0\\\\
\end{aligned}$
$x^{2}-16 x+64=48\\\\ $
$(x-8)^{2}=48\\\\ $
$x-8=\pm 4 \sqrt{3}\\\\ $
$x=8 \pm 4 \sqrt{3}\\\\ $
When $x=8-4 \sqrt{3}\\\\ $
$y=\dfrac{1}{4}(24-12 \sqrt{3}-28)\\\\ $
$=-1-3 \sqrt{3}\\\\ $
$\begin{aligned}
\text { When } x&=8+4 \sqrt{3}, \\\\
y &=\dfrac{1}{4}(24+12 \sqrt{3}-28) \\\\
&=-1+3 \sqrt{3}\\\\
\end{aligned}$
$\therefore$ The coordinates of the points $A$ and $B$ ane $(8-4 \sqrt{3}-1-3 \sqrt{3})$
and $(8+4 \sqrt{3},-1+3 \sqrt{3})$.
$\begin{aligned}
&\\
\therefore\ A B & =\sqrt{(8 \sqrt{3})^2+6(\sqrt{3})^2} \\\\
& =\sqrt{192+108} \\\\
& =\sqrt{300} \\\\
& =10 \sqrt{3}
\end{aligned}$
-

The points $R$ and $S$ lie on a circle with centre $C(a,-2)$,
as shown in the diagram.The point $R$ has coordinates $(2,3)$ and the point $S$
has coordinates $(10,1) .$ $M$ is the midpoint of the line segment $R S .$
The line $l$ passes through $M$ and $C .$
(a) Find an equation for $l .$
(b) Find the value of $a .$
(c) Find the equation of the circle.
(d) Find the points of intersection, $A$ and $B$, of the line $l$ and the circle.
SOLUTION
$M$ is the midpoint of $R S$.
$\begin{aligned}
&\\
\therefore\ M &=\left(\dfrac{2+10}{2}, \dfrac{3+1}{2}\right) \\\\
&=(6,2)\\\\
\end{aligned}$
Gradient of $R S=\dfrac{3-1}{2-10}=-\dfrac{1}{4}$
$\begin{aligned}
&\\
\therefore \text{Gradient of } l&=4\\\\
\end{aligned}$
Equation of $l$ is
$\begin{aligned}
&\\
y-2 &=4(x-6) \\\\
y &=4 x-22\\\\
\end{aligned}$
$l$ passes through $(a,-2)$
$\begin{aligned}
&\\
\therefore-2 &=4 a-22 \\\\
4 a &=20 \\\\
a &=5\\\\
\end{aligned}$
radius of circle $=R C$
$\begin{aligned}
&\\
&=\sqrt{(5-2)^{2}+(-2-3)^{2}} \\\\
&=\sqrt{34}\\\\
\end{aligned}$
The equation of circle is
$\begin{aligned}
&\\
(x-5)^{2}+(y+2)^{2}&=34\\\\
\end{aligned}$
When $l$ intersects the circle,
$\begin{aligned}
&\\
&(x-5)^{2}+(4 x-22+2)^{2}=34\\\\
&(x-5)^{2}+(4 x-22+2)^{2} =34 \\\\
&x^{2}-10 x+25+16 x^{2}-160 x+400-34=0 \\\\
&17 x^{2}-170 x+391 =0 \\\\
&x^{2}-10 x+23 =0 \\\\
&x^{2}-10 x+25 =2 \\\\
&(x-5)^{2} =2 \\\\
&x-5 =\pm \sqrt{2} \\\\
&x =5 \pm \sqrt{2}\\\\
\end{aligned}$
$\begin{aligned}
\text { When } x&=5-\sqrt{2}, \\\\
y &=4(5-\sqrt{2})-22 \\\\
&=-4 \sqrt{2}-2\\\\
\text { When } x&=5+\sqrt{2} \\\\
&y=4(5+\sqrt{2})-22 \\\\
&=4 \sqrt{2}-2 \\\\
\therefore\ A&=(5+\sqrt{2}, 4 \sqrt{2}-2) \\\\
B &=(5-\sqrt{2},-4 \sqrt{2}-2)
\end{aligned}$
-
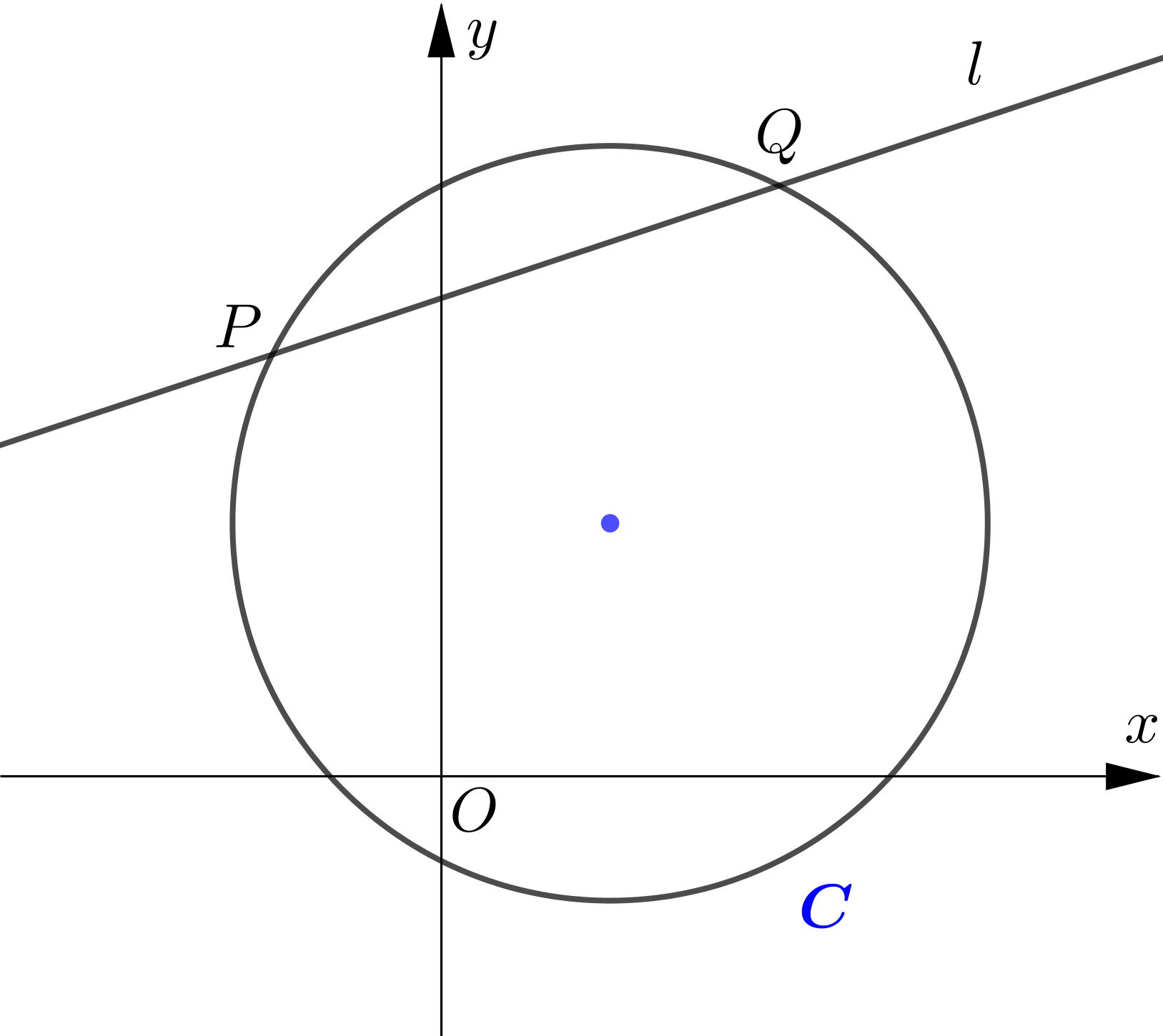
The circle $C$ has equation $x^{2}-4 x+y^{2}-6 y=7$. The line $l$ with equation $x-3 y+17=0$ intersects
the circle at the points $P$ and $Q$.
(a) Find the coordinates of the point $P$ and the point $Q$.
(b) Find the equation of the tangent at the point $P$ and the point $Q$.
(c) Find the equation of the perpendicular bisector of the chord $P Q$.
(d) Show that the two tangents and the perpendicular bisector intersect at a single point and find the coordinates of the point of intersection.
SOLUTION

$\begin{aligned}
&C: x^{2}-4 x+y^{2}-6 y=7 \\\\
&x^{2}-4 x+4+y^{2}-6 y+9=4+9+7 \\\\
&(x-2)^{2}+(y-3)^{2}=20 \\\\
&\therefore\ \text { centre: }(2,3) \\\\
&\text { radius }=\sqrt{20}\\\\
\end{aligned}$
Let the centre of the circle be $A$.
$\begin{aligned}
&\\
\text { gradient of } A P&=\dfrac{3-5}{2-(-2)}=-\dfrac{1}{2}\\\\
\end{aligned}$
gradient of tangent at $P=2$
$\begin{aligned}
&\\
\text { gradient of } A Q &=\dfrac{3-7}{2-4}=2\\\\
\end{aligned}$
gradient of tangent at $Q=-\dfrac{1}{2}\\\\ $
Equation of tangent at $P$ is
$\begin{aligned}
&\\
y-5 &=2(x+2) \\\\
y &=2 x+9\\\\
\end{aligned}$
Equation of tangent at $Q$ is
$\begin{aligned}
&\\
y-7&=-\dfrac{1}{2}(x-4) \\\\
y&=-\dfrac{1}{2} x+9\\\\
\end{aligned}$
Let the midpoint of $PQ$ be $M$.
$\begin{aligned}
&\\
\therefore\ M &=\left(\dfrac{-2+4}{2}, \dfrac{5+7}{2}\right) \\\\
&=(1,6)\\\\
\end{aligned}$
Gradient of $A M=\dfrac{3-6}{2-1}=-3\\\\ $
$\therefore$ Equation of the perpendicular bisector of $PQ$ is
$\begin{aligned}
&\\
y-6&=-3(x-1) \\\\
y&=-3 x+9\\\\
\end{aligned}$
At the point of intersection of two tangents,
$\begin{aligned}
&\\
2 x+9 &=-\dfrac{1}{2} x+9 \\\\
\therefore x&=0\\\\
\end{aligned}$
Substituting $x=0$ in $y=2 x+9\\\\ $,
$y=2(0)+9=9\\\\ $
The point of intersection of two tangents is $(0,9).\\\\ $
Substituting $x=0$ in $y=-3 x+9\\\\ $.
$y=-3(0)+9=9\\\\ $
$\therefore$ The two tangents and the perpendicular bisector intersect at a single point.
The point of intersection of the two tangents and the perpendicular bisector is $(0,9)$.
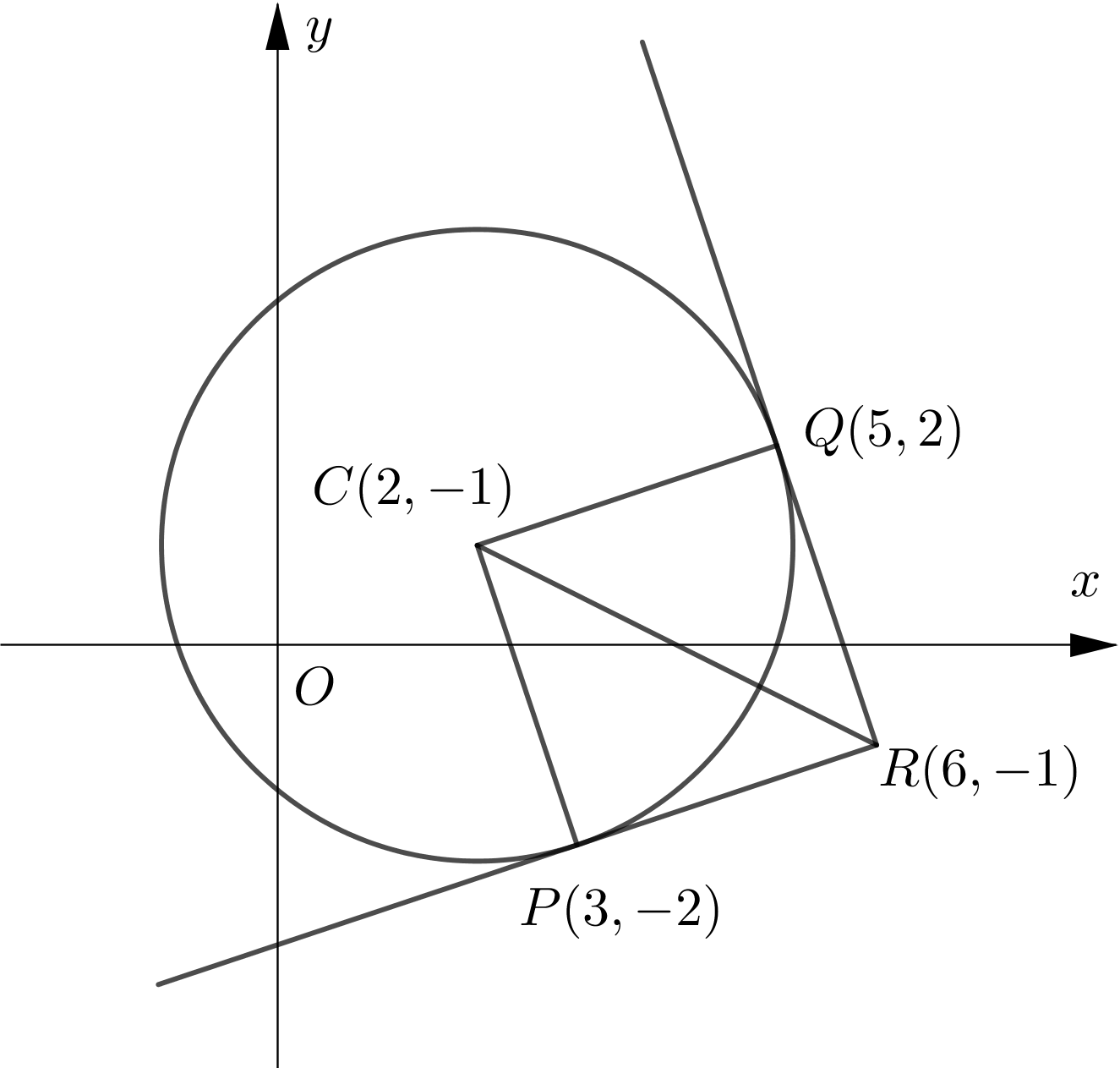
- The circle with centre $C$ has equation $(x-2)^{2}+(y-1)^{2}=10$.
The tangents to the circle at points $P$ and $Q$ meet at the point $R$ with coordinates $(6,-1)$.
(a) Show that $C P R Q$ is a square.
(b) Hence find the equations of both tangents.
SOUTION
$\begin{aligned}
\text { Circle: } & (x-2)^{2}+(y-1)^{2}=10 \\\\
\therefore\ \text{center}:\ & (2,1) \\\\
\text { radius }& =\sqrt{10} \\\\
C R &=\sqrt{(2-6)^{2}+(1+1)^{2}} \\\\
&=\sqrt{16+4} \\\\
&=\sqrt{20}\\\\
&=\sqrt{10} \sqrt{2} \\\\
&=\text { radius } \times \sqrt{2}\\\\
\end{aligned}$
Since radius $\perp$ tangent, $\triangle C P R$ and $\triangle C Q R$ are
$45^{\circ}-45^{\circ}$ right triangle.
$\begin{aligned}
&\\
\therefore\ & CPRQ \text{ is a square.}\\\\
\end{aligned}$
Let the tangent meet the circle at $P(a, b)$.
$\begin{aligned}
&\\
&(a-2)^{2}+(b-1)^{2}=10 \\\\
&a^{2}-4 a+4+b^{2}-2 b+1=10 \\\\
&a^{2}+b^{2}-4 a-2 b=5 ---(1)\\\\
&\text { Since } C P=P R, \\\\
&(a-6)^{2}+(b+1)^{2}=10 \\\\
&a^{2}-12 a+36+b^{2}+2 b+1=10 \\\\
&a^{2}+b^{2}-12 a+2 b=-27---(2)\\\\
&(1)-(2) \text{ yields}\\\\
&8 a-4 b=32\\\\
&2 a-b=8\\\\
&b=2 a-8\\\\
\end{aligned}$
substituting $b=2 a-8$ in eqn: $(1)$,
$\begin{aligned}
&\\
&a^{2}+(2 a-8)^{2}-4 a-2(2 a-8)=5 \\\\
&a^{2}+4 a^{2}-32 a+64-4 a-4 a+16-5=0\\\\
&5 a^{2}-40 a+75=0 \\\\
&a^{2}-8 a+15=0 \\\\
&a=3 \text { or } a=5 \\\\
&\text { When } a=3, b=-2 \\\\
&\text { When } a=5, b=2\\\\
\end{aligned}$
Let the coordinates of the point $P$ and $Q$ be $(3,-2)$ and $(5,2)\\\\\\ $.
gradient of $R P=\dfrac{-2+1}{3-6}=\dfrac{1}{3}\\\\ $
$\therefore$ gradient of $R Q=-3\quad (\because RP\perp RQ) \\\\ $
The equation of tangent $P R$ is
$\begin{aligned}
&\\
y+1 &=\dfrac{1}{3}(x-6) \\\\
y &=\dfrac{1}{3} x-3\\\\
\end{aligned}$
The equation of tangent $R Q$ is
$\begin{aligned}
&\\
y+1 &=-3(x-6) \\\\
y &=-3 x+17\\\\
\end{aligned}$
-
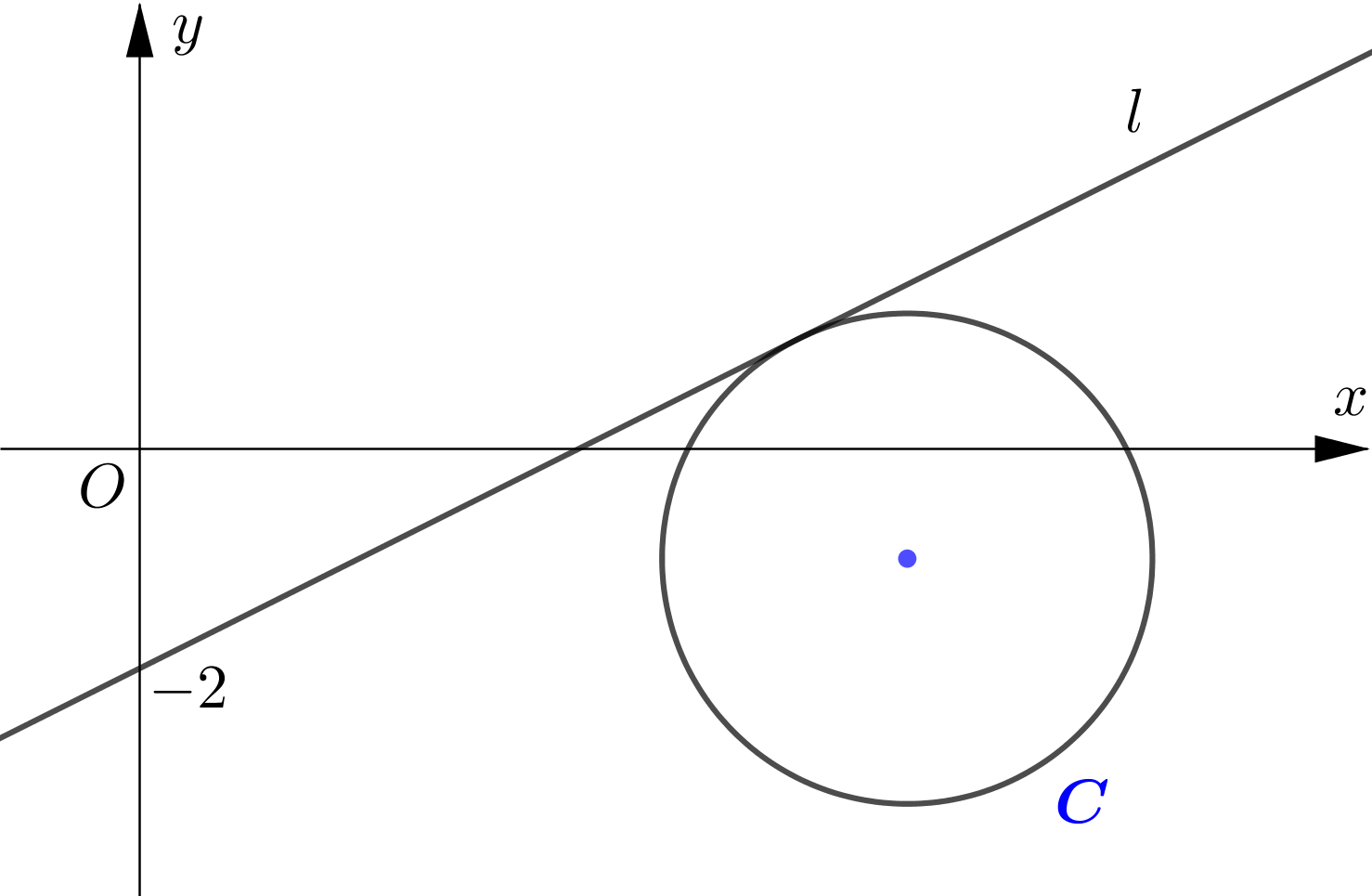
The circle $C$ has equation $(x-7)^{2}+(y+1)^{2}=5$.
The line $l$ with positive gradient passes through $(0,-2)$ and is a tangent to the circle.
Find an equation of $l$, giving your answer in the form $y=m x+c$.
SOLUTION
Circle: $(x-7)^{2}+(y+1)^{2}=5\\\\ $
Centre: $(7,-1)\\\\ $
Let $Q=(0,-2)$ and $l$ touch the circle at $(a, b).\\\\ $
$\therefore\ (a-7)^{2}+(b+1)^{2}=5\\\\ $
$a^{2}-14 a+49+b^{2}+2 b+1=5\\\\ $
$a^{2}+b^{2}-14 a+2 b=-45 --- (1)\\\\ $
$\begin{aligned}
P Q^{2} &=O Q^{2}-O P^{2} \\\\
a^{2}+(b+2)^{2} &=7^{2}+(-1+2)^{2}-5 \\\\
&=45 \\\\
a^{2}+b^{2}+4 b+4 &=45 \\\\
a^{2}+b^{2}+4 b &=41---(2)\\\\
\end{aligned}$
Subtracting eqn: (1) from equation(2),
$\begin{aligned}
&\\
14 a+2 b &=86 \\\\
7 a+b &=43 \\\\
b &=43-7 a\\\\
\end{aligned}$
Substitue $b=43-7 a$ in equation (2),
$\begin{aligned}
&\\
a^{2}+(43-7 a)^{2}+4(43-7 a)&=41 \\\\
50 a^{2}-630 a+1980&=0 \\\\
\therefore a=6 \text { or } a&=\dfrac{33}{5}\\\\
\end{aligned}$
When $a=6, b=1\\\\ $
When $a=\dfrac{33}{5}, b=-\dfrac{16}{5}\\\\ $
Since the gradient of $l=\dfrac{b+2}{a}>0\\\\ $,
we have to choose $a=6$and $b=1\\\\ $.
$\therefore$ gradient of $l=\dfrac{1+2}{6}=\dfrac{1}{2}\\\\ $
The line equation of $l$ is $y+2=\dfrac{1}{2} x \Rightarrow y=\dfrac{1}{2} x-2\\\\ $.

Post a Comment for "Analytic Geometry : The Circles"