Calculus Exercise (7) : Differentiation of Implicit Functions

Explicit Function

A function in which the dependent variable can be written explicitly in terms of the
independent variable.


For examples, $y = 3x^2 - 1, y = \sin 2x$, etc.
are explicit functions where $y$ is called the dependent variable
and $x$ is called the independent variable.

Implicit Functions

An implicit function is a function in which one variable cannot be explicitly expressed
in terms of the other.


For examples, $x^2y + xy^3= 3, x + y^2 = cos xy,$ etc. are implicit functions where
$y = f (x)$ but sometimes $y$ cannot be explicitly expressed in terms of $x$.

Differentiation of Implicit Functions

Since $y$ is a function of $x$, it is often easier to differentiate an implicit function
by differentiating each term in turn by applying the chain, product and quotient rules.

Problems

1. 
   Find $\dfrac{d y}{d x}.\\\\ $
   
   (a) $x y=5\\\\ $
   
   (b) $x(x+y)=y^{2}\\\\ $
   
   (c) $x^{2}-x y^{2}-y^{3}=2\\\\ $
   
   (d) $x^{3}-4 x y+y^{2}=14\\\\ $
   
   (e) $\dfrac{1}{x^{2}}+\dfrac{1}{y^{2}}=\dfrac{1}{4}\\\\ $
   
   (f) $x y-y^{2}+3 x=2\\\\ $
   
   (g) $\dfrac{1}{x^{3}}+\dfrac{1}{y^{3}}=\dfrac{1}{8}\\\\ $
   
   (h) $x^{2} y-x y^{2}+3 x=2\\\\ $
   
   (i) $2 y+5-x^{2}-y^{3}=0$
   



SOLUTION
$\begin{aligned}
\text{ (a) }\quad &x y=5\\\\
&\text { Differentiate with respect to } x.\\\\
&x \dfrac{d y}{d x}+y=0 \\\\
&\dfrac{d y}{d x}=-\dfrac{y}{x}\\\\
\text{ (b) }\quad &x(x+y)=y^{2}\\\\
&x^{2}+x y=y^{2}\\\\
&\text { Differentiate with respect to } x.\\\\
&2 x+x \dfrac{d y}{d x}+y=2 y \dfrac{d y}{d x} \\\\
&(2 y-x) \dfrac{d y}{d x}=2 x+y \\\\
&\dfrac{d y}{d x}=\dfrac{2 x+y}{2 y-x}\\\\
\text{ (c) }\quad & x^{2}-x y^{2}-y^{3}=2\\\\
&\text { Differentiate with respect to } x.\\\\
&2 x-2 x y \dfrac{d y}{d x}-y^{2}-3 y^{2} \dfrac{d y}{d x}=0 \\\\
&2 x-y^{2}=2 x y \dfrac{d y}{d x}+3 y^{2} \dfrac{d y}{d x} \\\\
&\left(2 x y-3 y^{2}\right) \dfrac{d y}{d x}=2 x-y^{2} \\\\
&\dfrac{d y}{d x}=\dfrac{2 x-y^{2}}{2 x y-3 y^{2}}\\\\
\text{ (d) }\quad & x^{3}-4 x y+y^{2}=14\\\\
&\text { Differentiate with respect to } x.\\\\
&3 x^{2}-4 x \dfrac{d y}{d x}-4 y+2 y \dfrac{d y}{d x}=0 \\\\
&3 x^{2}-4 y=4 x \dfrac{d y}{d x}-2 y \dfrac{d y}{d x} \\\\
&(4 x-2 y) \dfrac{d y}{d x}=3 x^{2}-4 y \\\\
&\dfrac{d y}{d x}=\dfrac{3 x^{2}-4 y}{4 x-2 y}\\\\
\text{ (e) }\quad & \dfrac{1}{x^{2}}+\dfrac{1}{y^{2}}=\dfrac{1}{4} \\\\
&\text { Differentiate with respect to } x.\\\\
&-\dfrac{2}{x^{3}}-\dfrac{2}{y^{3}} \dfrac{d y}{d x}=0 \\\\
&\dfrac{d y}{d x}=-\dfrac{y^{3}}{x^{3}}\\\\
\text{ (f) }\quad & x y-y^{2}+3 x=2 \\\\
&\text { Differentiate with respect to } x.\\\\
&x \dfrac{d y}{d x}+y-2 y \dfrac{d y}{d x}+3=0 \\\\
&(2 y-x) \dfrac{d y}{d x}=y+3 \\\\
&\dfrac{d y}{d x}=\dfrac{y+3}{2 y-x}\\\\
\text{ (g) }\quad & \dfrac{1}{x^{3}}+\dfrac{1}{y^{3}}=\dfrac{1}{8} \\\\
&\text { Differentiate with respect to } x.\\\\
&-\dfrac{3}{x^{4}}-\dfrac{3}{y^{4}} \dfrac{d y}{d x}=0 \\\\
&\dfrac{d y}{d x}=-\dfrac{y^{4}}{x^{4}}\\\\
\text{ (h) }\quad & x^{2} y-x y^{2}+3 x=2 \\\\
&\text { Differentiate with respect to } x.\\\\
&x^{2} \dfrac{d y}{d x}+2 x y-2 x y \dfrac{d y}{d x}-y^{2}+3=0 \\\\
&\left(x^{2}-2 x y\right) \dfrac{d y}{d x}=y^{2}-2 x y-3 \\\\
&\dfrac{d y}{d x}=\dfrac{y^{2}-2 x y-3}{x^{2}-2 x y}\\\\
\text{ (i) }\quad & 2 y+5-x^{2}-y^{3}=0 \\\\
&\text { Differentiate with respect to } x.\\\\
&2 \dfrac{d y}{d x}-2 x-3 y \dfrac{d y}{d x}=0 \\\\
&(2-3 y) \dfrac{d y}{d x}=2 x \\\\
&\dfrac{d y}{d x}=\dfrac{2 x}{2-3 y}
\end{aligned}$


2. 
   Given that $x^{2}+y^{2}=1$, show that $y y^{\prime \prime}+\left(y^{\prime}\right)^{2}+1=0$.
   
SOLUTION

$\begin{aligned}
&x^{2}+y^{2}=1\\\\
&\text { Differentiate with respect to } x.\\\\
&2 x+2 y y^{\prime}=0 \\\\
&y y^{\prime}+x=0\\\\
&\text { Differentiate with respect to } x.\\\\
&y y^{\prime \prime}+\left(y^{\prime}\right)^{2}+1=0
\end{aligned}$

3. 
   If $x^{2}-y^{2}=3$, show that $y^{2} y^{\prime \prime}+x y^{\prime}=y$.
   

SOLUTIOON
$\begin{aligned}
&x^{2}-y^{2}=3\\\\
&2 x-2 y y^{\prime}=0 \\\\
&x-y y^{\prime}=0 \\\\
&y y^{\prime}=x\\\\
&\text { Differentiate with respect to } x.\\\\
&y y^{\prime \prime}+y^{\prime} \cdot y^{\prime}=1 \\\\
&\therefore\ y^{2} y^{\prime \prime}+y y^{\prime} \cdot y^{\prime}=y \\\\
&\therefore\ y^{2} y^{\prime \prime}+x y^{\prime}=y \quad\left[\because y y^{\prime}=x\right]
\end{aligned}$

4. 
   Find the equation of the tangent line to the curve $3 x^{2}+2 y^{2}=3 x y+12$ at the point $(2,3)$.
   



SOLUTION



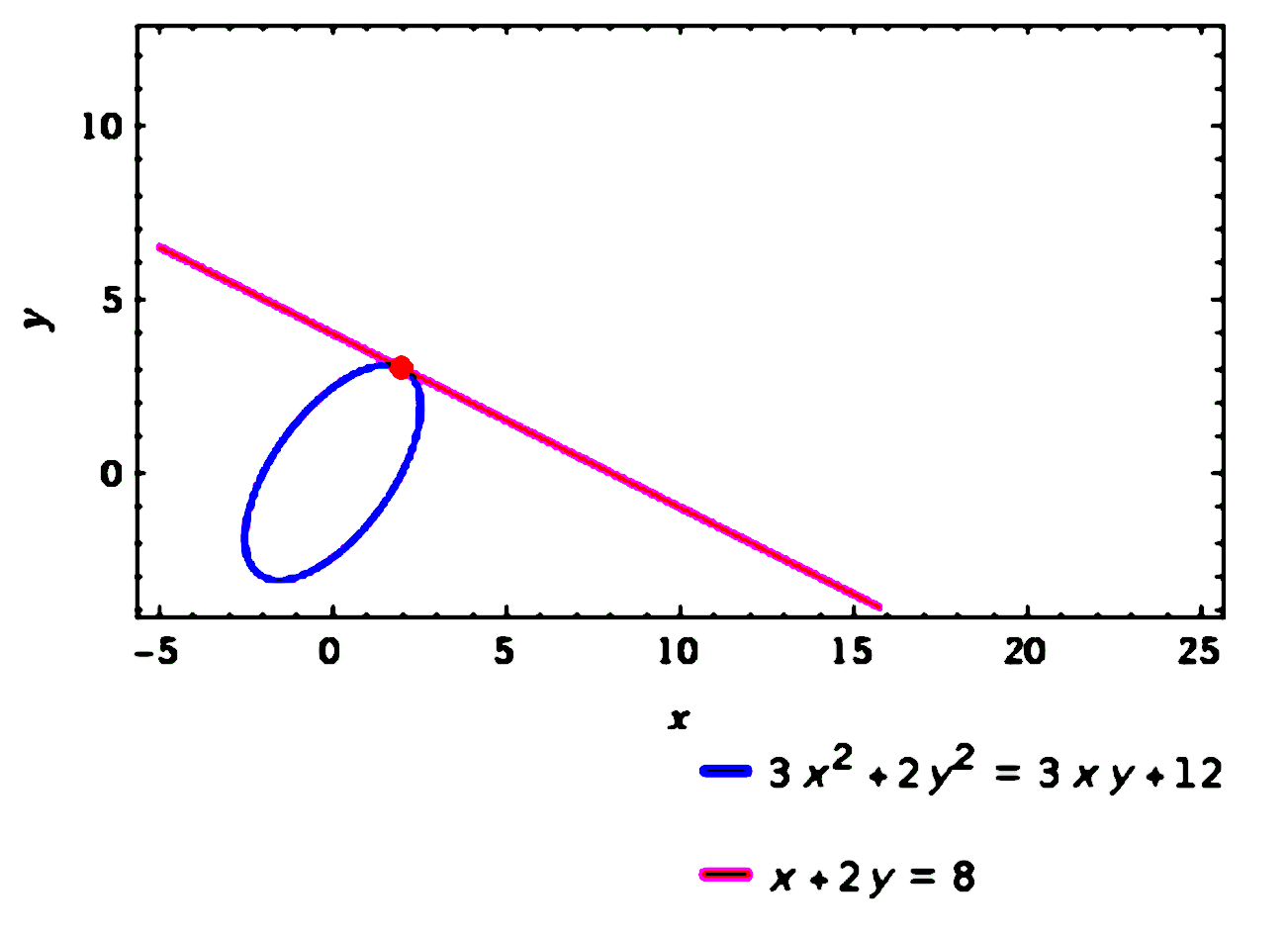
$\begin{aligned}
\text{ Curve } : & 3 x^{2}+2 y^{2}=3 x y+12\\\\
\text{ Differentiate } & \text{ with respect to } x.\\\\
(6 x+4 y) \dfrac{d y}{d x}&=3 x \dfrac{d y}{d x}+3 y \\\\
(4 y-3 x) \dfrac{d y}{d x}&=3 y-6 x \\\\
\therefore \dfrac{d y}{d x}&=\dfrac{3 y-6 x}{4 y-3 x} \\\\
\text { Let }\left(x_{1}, y_{1}\right)&=(2,3)\\\\
m&=\left.\dfrac{d y}{d x}\right|_{(2,3)}\\\\
&=\dfrac{3(3)-6(2)}{4(3)-3(2)}\\\\
&=-\dfrac{1}{2}\\\\
\end{aligned}$


$\therefore$ The equation of tangent at $\left(x_{1}, y_{1}\right)$ is


$\begin{aligned}
&\\\\
y-y_{1}&=m\left(x-x_{1}\right) \\\\
y-3&=-\dfrac{1}{2}(x-2) \\\\
x+2 y&=8
\end{aligned}$

5. 
   Show that the equation of the tangent to the curve $x^{2}+x y+y=0$
   at the point $(a, b)$ is $x(2 a+b)+y(a+1)+b=0$.
   



SOLUTION
$\begin{aligned}
\quad &\text{ Curve } : x^{2}+x y+y=0\\\\
\quad &\text{Differentiate with respect to } x.\\\\
\quad &2 x+x \frac{d y}{d x}+y+\frac{d y}{d x}=0 \\\\
\quad &(x+1) \frac{d y}{d x}=-(2 x+y) \\\\
\quad &\frac{d y}{d x}=-\frac{2 x+y}{x+1}\\\\
\end{aligned}$



The gradient of tangent at $(a, b)$ is


$\begin{aligned}
&\\
\quad \left.\frac{d y}{d x}\right|_{(a, b)}&=-\frac{2 a+b}{a+1}\\\\
\end{aligned}$


Since $(a, b)$ lies on the curve,


$\begin{aligned}
&\\
\quad & a^{2}+a b+b =0\\\\
\end{aligned}$



Hence the equation of tangent at $(a, b)$ is


$\begin{aligned}
&\\
\quad & y-b=-\frac{2 a+b}{a+1}(x-a) \\\\
\quad & y(a+1)-a b-b=-x(2 a+b)+2 a^{2}+a b \\\\
\quad & x(2 a+b)+y(a+1)-2 a^{2}-2 a b-b=0 \\\\
\quad & x(2 a+b)+y(a+1)-2 a^{2}-2 a b-2 b+b=0 \\\\
\quad & x(2 a+b)+y(a+1)-2\left(a^{2}+a b+b\right)+b=0 \\\\
\therefore\ & x(2 a+b)+y(a+1)-2(0)+b=0 \\\\
\therefore\ & x(2 a+b)+y(a+1)+b=0
\end{aligned}$

6. 
   Find the coordinates of the points on the curve $x^{2}-y^{2}=3 x y-39$ at which
   the tangents are (i) parallel (ii) perpendicular to the line $x+y=1$.
   

SOLUTION



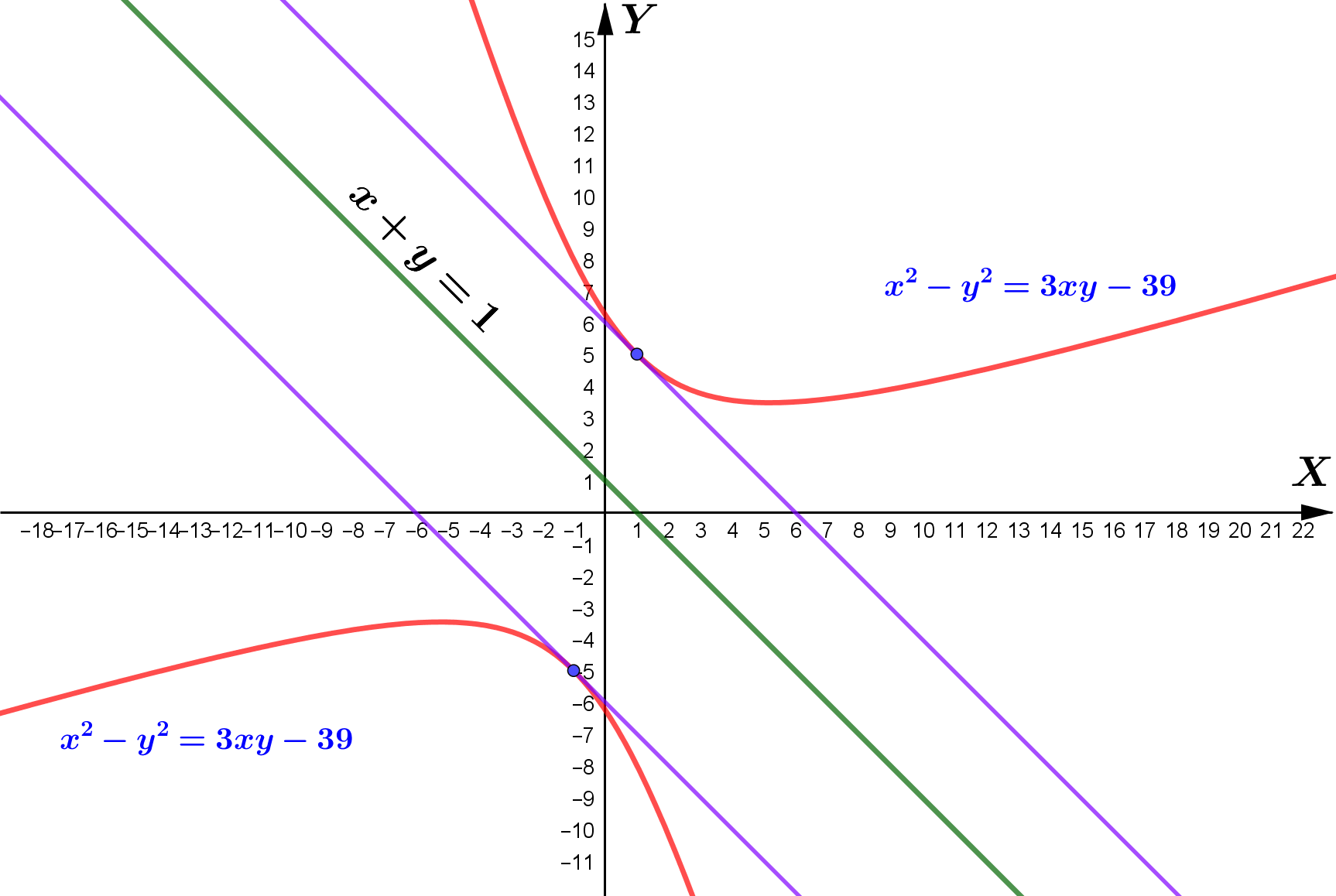
Curve: $x^{2}-y^{2}=3 x y-39\\\\ $


Differentiate with respect to $x$.


$\begin{aligned}
&\\
\quad &2 x-2 y \frac{d y}{d x}=3 x \frac{d y}{d x}+3 y \\\\
\quad &(3 x+2 y) \frac{d y}{d x}=2 x-3 y \\\\
\quad &\frac{d y}{d x}=\frac{2 x-3 y}{3 x+2 y}\\\\
\end{aligned}$


Line: $x+y=1 \Rightarrow y=1-x\\\\ $


$\therefore$ The gradient of line $=-1\\\\ $


(i) tangent // given line


$\begin{aligned}
&\\
\quad & \frac{2 x-3 y}{3 x+2 y}=-1 \\\\
\quad & 2 x-3 y=-3 x-2 y \\\\
\quad & y=5 x \\\\
\therefore\ & x^{2}-(5 x)^{2}=3 x(5 x)-39 \\\\
&\quad x^{2}-25 x^{2}=15 x^{2}-39 \\\\
\therefore\ & x^{2}=1 \\\\
& x=\pm 1\\\\
\therefore\ & y=\pm 5\\\\
\end{aligned}$


Thus, the points on the curve at
which the tangents are parallel to the
line $x + y = 1$ are $(-1, -5)$ and $(1, 5)$.


(ii) tangent $\perp$ given line



$\begin{aligned}
&\\
\quad & \frac{2 x-3 y}{3 x+2 y}=1 \\\\
\quad & 2 x-3 y=3 x+2 y \
\quad & x=-5 y \\\\
\therefore\ &(-5 y)^{2}-y^{2}=3(-5 y) y-39 \\\\
\quad & 25 y^{2}-y^{2}=-15 y^{2}-39 \\\\
\quad & y^{2}=-1\\\
\end{aligned}$


Since $y^{2}>0$ for all $y \in \mathbb{R}, y^{2}=-1$ is impossible.


Therefore, there is no tangent on the curve which is
parallel to the line $x+y=1$.

7. 
   The equation of a curve is $x y(x+y)=2 a^{3}$, where $a$ is a non-zero constant. Show that
   there is only one point on the curve at which the tangent is parallel to the $x$ axis,
   and find the coordinates of this point.
   

SOLUTION
Curve: $y=(x+2 a)^{3} $


$\begin{aligned}
&\\
\text{ When } y & =a^{3},(x+2 a)^{3}=a^{3}\\\\
x+2 a &=a \\\\
x&=-a\\\\
\end{aligned}$


Thus, $\left(-a, a^{3}\right)$ is the point on the curve where the
tangent exists.


$\begin{aligned}
&\\
\frac{d y}{d x}&=\frac{d}{d x}(x+2 a)^{3}\\\\
&=3(x+2 a)^{2} \frac{d}{d x}(x+2 a)\\\\
&=3(x+2 a)^{2}(1)=3(x+2 a)^{2} \\\\
m &=\left.\frac{d y}{d x}\right|_{\left(-a, a^{3}\right)}\\\\
&=3(-a+2 a)^{2}=3 a^{2}\\\\
\end{aligned}$


$\therefore$ The equation of tangent at $\left(-a, a^{3}\right)$ is


$\begin{aligned}
&\\
y-a^{3}&=m(x-(-a))\\\\
y-a^{3}&=3 a^{2}(x-(-a)) \\\\
y&=3 a^{2} x+4 a^{3}
\end{aligned}$

8. 
   Show that the tangent lines to the curve $x^{2}-x y+y^{2}=3$,
   at the points where the curve cuts the $x$ axis, are parallel to each other.
   



SOLUTION



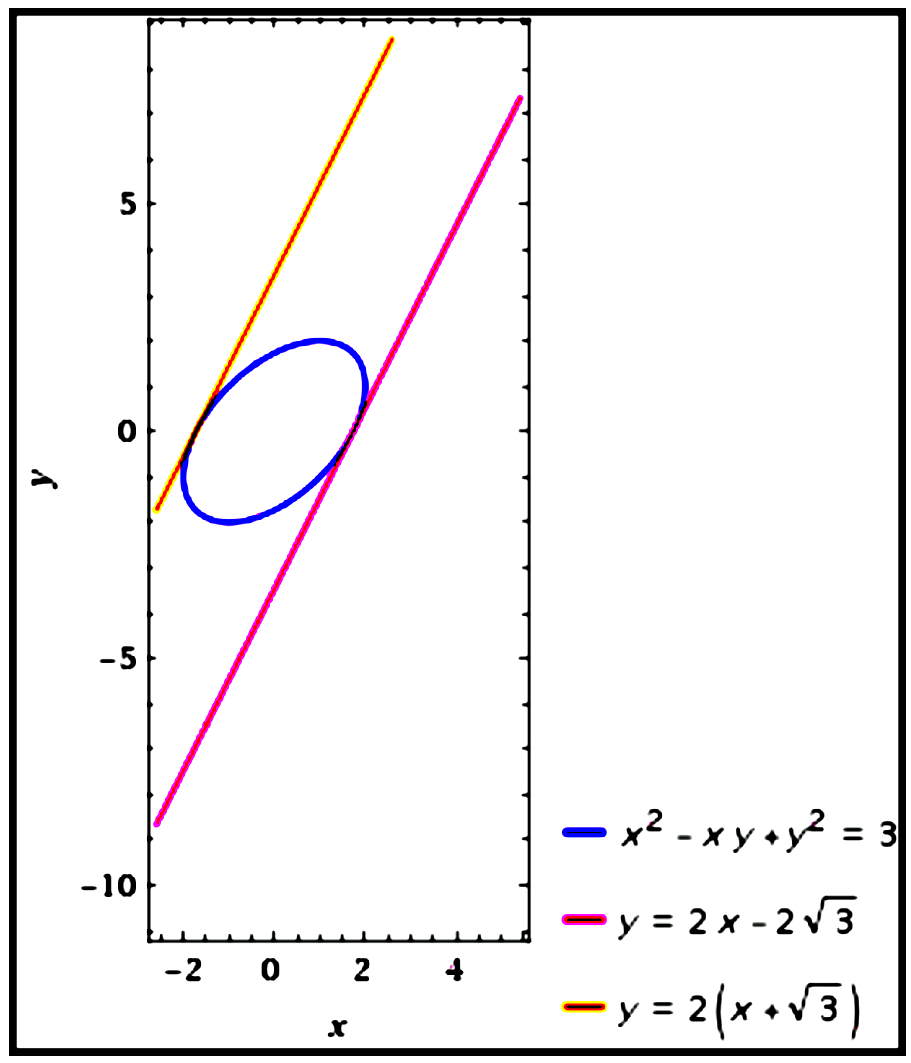
Curve $: x^{2}-x y+y^{2}=3\\\\ $


Differentiate with respect to $x$.


$\begin{aligned}
&\\
2 x-x \frac{d y}{d x}-y+2 y \frac{d y}{d x}&=0 \\\\
(2 y-x) \frac{d y}{d x}&=y-2 x \\\\
\frac{d y}{d x}&=\frac{y-2 x}{2 y-x}\\\\
\end{aligned}$


When the curve cuts the $x$ axis,


$\begin{aligned}
&\\
y&=0 \\\\
x^{2}&=3\\\\
x&=\pm \sqrt{3}\\\\
\end{aligned}$


$\therefore$ The curve cuts the $x$-axis at
$(-\sqrt{3}, 0)$ and $(\sqrt{3}, 0)$.


$\begin{aligned}
&\\
\therefore\ &\text{ At }(-\sqrt{3}, 0), \\\\
m_{1}&=\left.\frac{d y}{d x}\right|_{(-\sqrt{3}, 0)}\\\\
&=\frac{0-2(-\sqrt{3})}{2(0)-(-\sqrt{3})}\\\\
&=2\\\\
\therefore\ & \text{ At } (\sqrt{3}, 0),\\\\
m_{2}&=\left.\frac{d y}{d x}\right|_{(\sqrt{3}, 0)}\\\\
&=\frac{0-2(\sqrt{3})}{2(0)-(\sqrt{3})}\\\\
&=2\\\\
\therefore\ m_{1}&=m_{2}\\\\
\end{aligned}$


Hence, The two tangents are parallel.

9. 
   Show that the equation of the tangent line to the curve $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$
   at $(p, q)$ is $\dfrac{p x}{a^{2}}+\dfrac{q y}{b^{2}}=1$.
   


SOLUTION
$\begin{aligned}
\text{Curve }: &\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\\\\
\text{At } (p, q), & \frac{p^{2}}{a^{2}}+\frac{q^{2}}{b^{2}}=1\\\\
\text{Differentiate } & \text{ with respect to } x.\\\\
\frac{2 x}{a^{2}}+\frac{2 y}{b^{2}} \cdot \frac{d y}{d x} &=0 \\\\
\frac{d y}{d x}& =-\frac{b^{2} x}{a^{2} y}\\\\
\text{At } (p, q), &\\\\
\left.\frac{d y}{d x}\right|_{(p, q)}&=-\frac{b^{2} p}{a^{2} q}\\\\
\text{The equation } & \text{ of tangent at } (p, q) \text{ is}\\\\
y-q&=-\frac{b^{2} p}{a^{2} q}(x-p)\\\\
\text{Multiplying } & \text{ both sides with } \frac{q}{b^{2}},\\\\
\frac{q y}{b^{2}}-\frac{q^{2}}{b^{2}}&=-\frac{p x}{a^{2}}+\frac{p^{2}}{a^{2}} \\\\
\frac{p x}{a^{2}}+\frac{q y}{b^{2}}&=\frac{p^{2}}{a^{2}}+\frac{q^{2}}{b^{2}} \\\\
\therefore \frac{p x}{a^{2}}+\frac{q y}{b^{2}}&=1 \quad \left[\because \frac{p^{2}}{a^{2}}+\frac{q^{2}}{b^{2}}=1\right]
\end{aligned}$

10. 
    Show that the equation of the tangent line to the curve
    $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ at $(m, n)$ is $\dfrac{m x}{a^{2}}-\dfrac{n y}{b^{2}}=1 .$
    

SOLUTION
$\begin{aligned}
\text{Curve }: \qquad & \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\\\\
\text{At } (m, n),\qquad & \frac{m^{2}}{a^{2}}-\frac{n^{2}}{b^{2}}=1\\\\
\text{Differentiate } & \text{ with respect to } x.\\\\
\frac{2 x}{a^{2}}-\frac{2 y}{b^{2}} \cdot \frac{d y}{d x} &=0 \\\\
\frac{d y}{d x} &=\frac{b^{2} x}{a^{2} y} \\\\
\text { At } & (m, n),\\\\
\left.\frac{d y}{d x}\right|_{(m, n)} &=\frac{b^{2} m}{a^{2} n}\\\\
\text{The equation } & \text{ of tangent at } (m, n) \text{ is}\\\\
y-n &=\frac{b^{2} m}{a^{2} n}(x-m)\\\\
\text{Multiplying } & \text{ both sides with } \frac{n}{b^{2}},\\\\
\frac{n y}{b^{2}}-\frac{n^{2}}{b^{2}} &=\frac{m x}{a^{2}}-\frac{m^{2}}{a^{2}} \\\\
\frac{m x}{a^{2}}-\frac{n y}{b^{2}} &=\frac{m^{2}}{a^{2}}-\frac{n^{2}}{b^{2}} \\\\
\therefore \frac{m x}{a^{2}}-\frac{n y}{b^{2}} &=1 \quad\left[\because \frac{m^{2}}{a^{2}}-\frac{n^{2}}{b^{2}}=1\right]
\end{aligned}$


11. 
    Show that the tangents to each curve $2 x^{2}+y^{2}=6$ and $y^{2}=4 x$ at
    the point of intersection of the two curves are perpendicular to each other.
    

SOLUTION



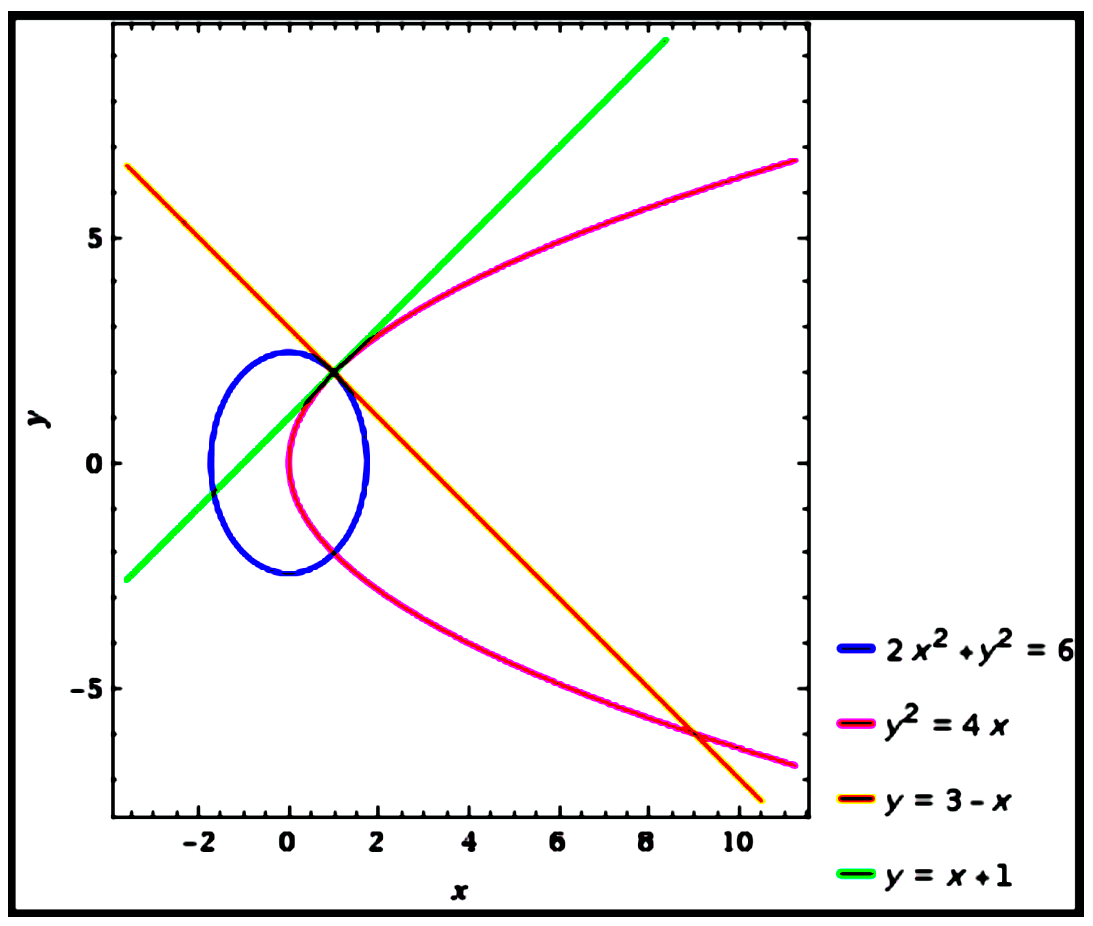
Curve 1: $2 x^{2}+y^{2}=6\\\\ $


Differentiate with respect to $x$.


$\begin{aligned}
&\\
4 x+2 y \frac{d y}{d x}=0\\\\
\frac{d y}{d x}=-\frac{2 x}{y}\\\\
\end{aligned}$



Curve 2: $y^{2}=4 x\\\\ $


Differentiate with respect to $x$.


$\begin{aligned}
&\\
2 y \frac{d y}{d x}=4 \\\\
\frac{d y}{d x}=\frac{2}{y}\\\\
\end{aligned}$



At the point of intersection of two curves,


$\begin{aligned}
&\\
2 x^{2}+4 x &=6 \\\\
x^{2}+2 x-3 &=0 \\\\
\therefore\ (x+3)(x-1)&=0 \\\\
\therefore\ x =-3 \text { or } x&=1\\\\
\end{aligned}$


When $x=-3, y^{2}=4(-3)=-12 \notin \mathrm{R} \text{(reject)}\\\\ $


When $x=1, y^{2}=4(1)=2\\\\ $


Thus, the point of intersection of the two curves is $(1,2)\\\\ $.


At $(1,2)$, gradient of Curve 1 $=m_{1}=-\frac{2}{2}=-1\\\\ $


At $(1,2)$, gradient of Curve 2 $=m_{2}=\frac{2}{2}=1\\\\ $


$\therefore m_{1} m_{2}=-1(1)=-1\\\\ $


Therefore, the tangents to each curve $2 x^{2}+y^{2}=6$ and $y^{2}=4 x$ at the point of intersection of the two curves are perpendicular to each other.

12. 
    Let $l$ be any tangent line to the curve $\sqrt{x}+\sqrt{y}=\sqrt{c}$ where $c$ is a non-zero constant.
    If $l$ cuts the $x$-axis at $(a, 0)$ and the $y$-axis at $(0, b)$, show that $a+b=c$.
    

SOLUTION
Curve: $\sqrt{x}+\sqrt{y}=\sqrt{c}$


Differentiate with respect to $x$.


$\begin{aligned}
&\\
\frac{1}{2 \sqrt{x}}+\frac{1}{2 \sqrt{y}} \cdot \frac{d y}{d x}&=0 \\\\
\frac{d y}{d x}&=-\frac{\sqrt{y}}{\sqrt{x}}\\\\
\end{aligned}$


Let $\left(x_{1}, y_{1}\right)$ be any point on the curve.


$\begin{aligned}
&\\
\therefore \sqrt{x_{1}}+\sqrt{y_{1}}&=\sqrt{c} \\\\
\left.\frac{d y}{d x}\right|_{\left(x_{1}, y_{1}\right)}&=-\frac{\sqrt{y_{1}}}{\sqrt{x_{1}}}\\\\
\end{aligned}$



The equation of tangent at $\left(x_{1}, y_{1}\right)$ is


$\begin{aligned}
&\\
y-y_{1}=-\frac{\sqrt{y_{1}}}{\sqrt{x_{1}}}\left(x-x_{1}\right)\\\\
\end{aligned}$


The tangent cuts $x$-axis at $(a, 0)$ and $y$-axis at $(0, b)$.


$\begin{aligned}
&\\
\therefore 0-y_{1}&=-\frac{\sqrt{y_{1}}}{\sqrt{x_{1}}}\left(a-x_{1}\right) \\\\
a&=x_{1}+\sqrt{x_{1} y_{1}} \\\\
\therefore b-y_{1}&=-\frac{\sqrt{y_{1}}}{\sqrt{x_{1}}}\left(0-x_{1}\right)\\\\
b&=y_{1}+\sqrt{x_{1} y_{1}} \\\\
\therefore\ a+b&=x_{1}+2 \sqrt{x_{1} y_{1}}+y_{1} \\\\
a+b&=\left(\sqrt{x_{1}}\right)^{2}+2 \sqrt{x_{1} y_{1}}+\left(\sqrt{y_{1}}\right)^{2} \\\\
a+b&=\left(\sqrt{x_{1}}+\sqrt{y_{1}}\right)^{2} \\\\
a+b&=(\sqrt{c})^{2} \\\\
\therefore\ a+b&=c
\end{aligned}$

13. 
    Find the normals to the curve $x y+2 x-y=0$ that are parallel to the line $2 x+y=0$.
    



SOLUTION



$\begin{aligned}
\text{Curve }: x y+2 x-y=0\\\\
\text{Differentiate with respect to } x.\\\\
x \frac{d y}{d x}+y+2-\frac{d y}{d x}&=0 \\\\
(1-x) \frac{d y}{d x}&=y+2 \\\\
\frac{d y}{d x}&=\frac{y+2}{1-x} \\\\
\therefore \text { Gradient of tangent }&=\frac{2+y}{1-x} \\\\
\therefore \text { Gradient of normal }&=-\frac{1}{\frac{d y}{d x}} \\\\
&=\frac{x-1}{y+2}\\\\
\text{Line }: 2 x+y&=0\\\\
\therefore\ y&=-2 x\\\\
\therefore\ \text{ Gradient of line } &=-2\\\\
\end{aligned}$


Since normals $\parallel$ given line,


$\begin{aligned}
\frac{x-1}{y+2}&=-2 \\\\
\therefore\ x&=-2 y-3
\end{aligned}$


Substituting $x=-2, y-3$ in curve equation,


$\begin{aligned}
&\\
(-2 y-3) y+2(-2 y-3)-y&=0 \\\\
\therefore\ y^{2}+4 y+3&=0 \\\\
\therefore\ (y+3)(y+1)&=0 \\\\
\therefore\ y=-3 \text { or } y&=-1\\\\
\text{When } y=-3,\quad x&=3\\\\
\text{When } y=-1,\quad x&=-1\\\\
\end{aligned}$


The equation of normal line


$\begin{aligned}
&\\
&(-1,-1) \text { is } y+1=-2(x+1) \\\\
&\therefore \quad 2 x+y+3=0\\\\
\end{aligned}$


The equation of normal line at $(3,-3)$ is


$\begin{aligned}
&\\
y+3&=-2(x-3) \\\\
\therefore\ 2 x+y-3&=0\\\\
\end{aligned}$

14. 
    If $f(x)+x^{2}[f(x)]^{3}=10$ and $f(1)=2$, find $f^{\prime}(1)$.
    

SOLUTION
$\begin{aligned}
f(x)+x^{2}[f(x)]^{3} &=10 \\\\
\text { Differentiate with respect to } & x . \\\\
f^{\prime}(x)+3 x^{2}[f(x)]^{2} \cdot f^{\prime}(x)+2 x[f(x)]^{3} &=0 \\\\
f(1) &=2 \quad \text { (given) } \\\\ \text { When } x &=1 \\\\
\therefore\ f^{\prime}(1)+3(1)^{2}[f(1)]^{2} \cdot f^{\prime}(1)+2(1)[f(1)]^{3} &=0 \\\\ \therefore\ f^{\prime}(1)+3(1)^{2}[2]^{2} \cdot f^{\prime}(1)+2(1)[2]^{3} &=0 \\\\
\therefore\ f^{\prime}(1)+12 f^{\prime}(1)+16 &=0 \\\\
\therefore\ 13 f^{\prime}(1) &=-16 \\\\
\therefore\ f^{\prime}(1) &=-\frac{16}{13}
\end{aligned}$

15. 
    If $L$ is any normal line to the curve $x^{2}+y^{2}=1$, show that $L$ passes through the origin.
    



SOLUTION
Curve: $x^{2}+y^{2}=1$


Differentiate with respect to $x$.


$\begin{aligned}
&\\
2 x+2 y \frac{d y}{d x}&=0 \\\\
\frac{d y}{d x}&=-\frac{x}{y} \\\\
\therefore \text { Gradient of tangent }&=-\frac{x}{y}\\\\
\therefore \text { Gradient of normal }&=\frac{y}{x}\\\\
\end{aligned}$


Let $(a, b)$ be any point on the curve.


$\begin{aligned}
&\\\\
\therefore a^{2}+b^{2}&=1\\\\
b^{2}&=1-a^{2}\\\\
\end{aligned}$


Gradient of normal at $(a, b)=\dfrac{b}{a}$


Equation of normal at $(a, b)$ is


$\begin{aligned}
&\\
y-b&=\frac{b}{a}(x-a) \\\\
\therefore\ L: y&=\frac{b}{a} x\\\\
\text{When } x=0, y&=0\\\\
\end{aligned}$


$\therefore\ L$ passes through the origin.


16. 
    Where does the normal line to the curve $x^{2}-x y+y^{2}=3$ at the point
    $(-1,1)$ intersect the curve a second time?
    


SOLUTION



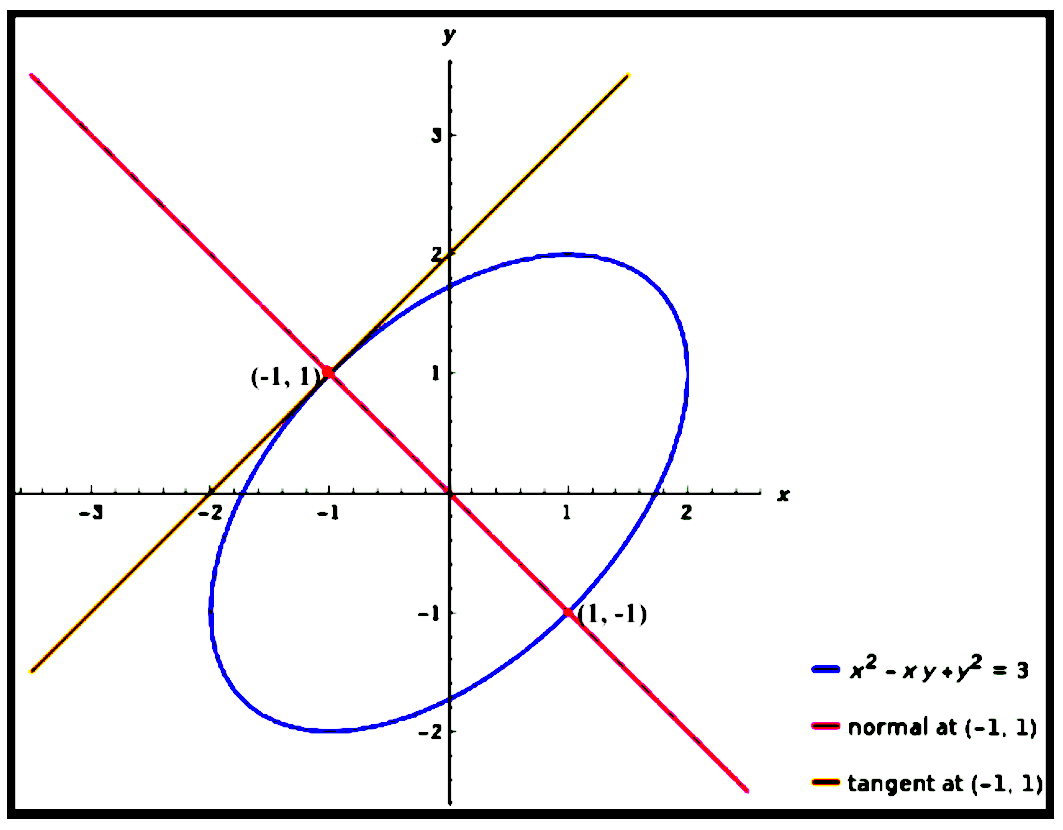
Curve: $x^{2}-x y+y^{2}=3\\\\ $


Differentiate with respect to $x$.


$\begin{aligned}
&\\
2 x-x \frac{d y}{d x}-y+2 y \frac{d y}{d x}&=0 \\\\
\frac{d y}{d x}&=\frac{2 x-y}{x-2 y} \\\\
\text { At } (-1,1),& \\\\
\text { Gradient of tangent } &=\frac{d y}{d x} \\\\
&=\frac{2(-1)-1}{-1-2(1)} \\\\
&=1\\\\
\therefore \text { Gradient of normal }&=-1\\\\
\end{aligned}$


Let $(a, b)$ be a point on the curve that the normal
intersect the curve a second time.


$\begin{aligned}
&\\
\therefore \frac{b-1}{a+1}=-1 \\\\
b=-a\\\\
\end{aligned}$


Since $(a, b)$ lies on the curve, $a^{2}-a b+b^{2}=3$.


$\begin{aligned}
&\\
\therefore a^{2}-a(-a)+(-a)^{2}&=3 \\\\
\therefore 3 a^{2}&=3 \\\\
a^{2}&=1 \\\\
\therefore a&=\pm 1\\\\
\text{ When } a=1, b=-1\\\\
\end{aligned}$


$\therefore$ The second point of intersection of normal and
the curve is $(1,-1)$.

Share :